
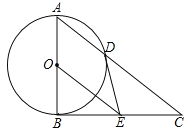
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CDOE;
(3)若![]() ,求OE的长.
,求OE的长.
【答案】(1)DE为⊙O的切线,理由见解析;(2)证明见解析;(3)OE =![]() .
.
【解析】试题分析:(1)连接OD,BD,由直径所对的圆周角是直角得到∠ADB为直角,可得出△BCD为直角三角形,E为斜边BC的中点,由直角三角形斜边上的中线等于斜边的一半,得到CE=DE,从而得∠C=∠CDE,再由OA=OD,得∠A=∠ADO,由Rt△ABC中两锐角互余,从而可得∠ADO与∠CDE互余,可得出∠ODE为直角,即DE垂直于半径OD,可得出DE为⊙O的切线;
(2)由已知可得OE是△ABC的中位线,从而有AC=2OE,再由∠C=∠C,∠ABC=∠BDC,可得△ABC∽△BDC,根据相似三角形的对应边的比相等,即可证得;
(3)在直角△ABC中,利用勾股定理求得AC的长,根据三角形中位线定理OE的长即可求得.
试题解析:(1)DE为⊙O的切线,理由如下:
连接OD,BD,

∵AB为⊙O的直径,
∴∠ADB=90°,
在Rt△BDC中,E为斜边BC的中点,
∴CE=DE=BE=![]() BC,
BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠C+∠A=90°,
∴∠ADO+∠CDE=90°,
∴∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为⊙O的切线;
(2)∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴![]() ,即BC2=ACCD.
,即BC2=ACCD.
∴BC2=2CDOE;
(3)解:∵cos∠BAD=![]() ,
,
∴sin∠BAC=![]() ,
,
又∵BE=![]() ,E是BC的中点,即BC=
,E是BC的中点,即BC=![]() ,
,
∴AC=![]() .
.
又∵AC=2OE,
∴OE=![]() AC=
AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=50°,∠DOE=35°,求∠BOD的度数;
(2)若∠AOE=160°,∠COD=40°,求∠AOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
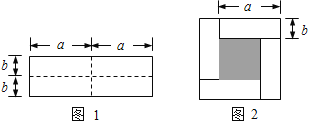
(1)图2的阴影部分的正方形的边长是 ______.
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = _____________;
= _____________;
(方法2)![]() =______________;
=______________;
(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() (如图),点
(如图),点![]() 分别在边
分别在边![]() 上,且四边形
上,且四边形![]() 是菱形
是菱形
(1)请使用直尺与圆规,分别确定点![]() 的具体位置(不写作法,保留画图痕迹);
的具体位置(不写作法,保留画图痕迹);
(2)如果![]() ,点
,点![]() 在边
在边![]() 上,且满足
上,且满足![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)当![]() 时,求
时,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在梯形![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上,联结
上,联结![]() ,过点
,过点![]() 作
作![]() 的垂线,交直线
的垂线,交直线![]() 与点
与点![]() ,
,



(1)如图1,已知![]() ,:求证:
,:求证:![]() ;
;
(2)已知:![]() ,
,
① 当点![]() 在线段
在线段![]() 上,求证:
上,求证:![]() ;
;
② 当点![]() 在射线
在射线![]() 上,①中的结论是否成立?如果成立,请写出证明过程;如果不成立,简述理由.
上,①中的结论是否成立?如果成立,请写出证明过程;如果不成立,简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭,小明家中买了一辆小轿车,他连续记录了![]() 天中每天行驶的路程(如下表),以
天中每天行驶的路程(如下表),以![]() 为标准,多于
为标准,多于![]() 的记为“
的记为“![]() ”,不足
”,不足![]() 的记为“
的记为“![]() ”,刚好
”,刚好![]() 的记为“
的记为“![]() ”.
”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程 |
|
|
|
|
|
|
|
(1)请求出这![]() 天中平均每天行驶多少千米?
天中平均每天行驶多少千米?
(2)若每行驶![]() 需用汽油
需用汽油![]() 升,汽油价
升,汽油价![]() 元/升,计算小明家这
元/升,计算小明家这![]() 天的汽油费用大约是多少元?
天的汽油费用大约是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC中,AB=AC,点D是AC上一点。点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于点F,连接CF
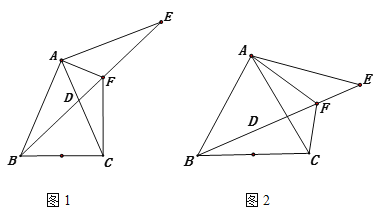
(1)如图1,找到与∠CFB相等的角,并证明
(2)如图2,如当∠ABC=60°,AF=m,EF=n时,求FB的长(用含m、n的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com