
【题目】在梯形![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上,联结
上,联结![]() ,过点
,过点![]() 作
作![]() 的垂线,交直线
的垂线,交直线![]() 与点
与点![]() ,
,



(1)如图1,已知![]() ,:求证:
,:求证:![]() ;
;
(2)已知:![]() ,
,
① 当点![]() 在线段
在线段![]() 上,求证:
上,求证:![]() ;
;
② 当点![]() 在射线
在射线![]() 上,①中的结论是否成立?如果成立,请写出证明过程;如果不成立,简述理由.
上,①中的结论是否成立?如果成立,请写出证明过程;如果不成立,简述理由.
【答案】(1)证明见解析;
(2)①证明见解析;②结论仍然成立,证明见解析.
【解析】
(1)过F作FM⊥AD,交AD的延长线于点M,通过AAS证明△ABE≌△EMF,根据全等三角形的性质即可得出AB=AD;
(2)①在AB上截取AG=AE,连接EG.通过ASA证明△BGE≌△EDF,根据全等三角形的性质即可得出BE=EF;
②
(1)如图:
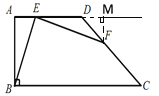
过F作FM⊥AD,交AD的延长线于点M,
∴∠M=90°,
∵∠BEF=90°,
∴∠AEB+MEF=90°,
∵∠A=90°,
∴∠ABE+∠AEB=90°,
∴∠MEF=∠ABE,
在△ABE和△EMF中,
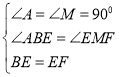 ,
,
∴△ABE≌△EMF(AAS)
∴AB=ME,AE=MF,
∵AM∥BC,∠C=45°,
∴∠MDF=∠C=45°,
∴∠DFM=45°,
∴DM=FM,
∴DM=AE,
∴DM+ED=AE+ED,
即AD=EM,
∴AB=AD;
(2)①证明:如图,
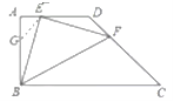
在AB上截取AG=AE,连接EG,则∠AGE=∠AEG,
∵∠A=90°,∠A+∠AGE+∠AEG=180°,
∴∠AGE=45°,
∴∠BGE=135°,
∵AD∥BC,
∴∠C+∠D=180°,
又∵∠C=45°,
∴∠D=135°,
∴∠BGE=∠D,
∵AB=AD,AG=AE,
∴BG=DE,
∵EF⊥BE,
∴∠BEF=90°,
又∵∠A+∠ABE+∠AEB=180°,
∠AEB+∠BEF+∠DEF=180°,
∠A=90°,
∴∠ABE=∠DEF,
在△BGE与△EDF中,
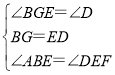 ,
,
∴△BGE≌△EDF(ASA),
∴BE=EF;
②结论仍然成立,证明如下,
如图:
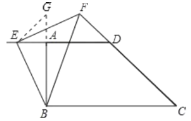
延长BA到点G,使BG=ED,连接EG,
则△EAG是等腰直角三角形,
∴∠EGB=45°,
∵ED∥BC,∠C=45°,
∴∠FDE=45°,
∴∠FDE=45°,
∴∠EGB=∠FDE,
∵∠A=90°,
∴∠AEB+∠ABE=90°,
∵EF⊥EB,
∴∠FED+∠AEB=90°,
∴∠AEB=∠FED,
在△BGE与△EFD中,
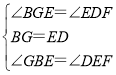 ,
,
∴△BGE≌△EDF(ASA),
∴BE=EF.


科目:初中数学 来源: 题型:
【题目】雾霾天气持续笼罩我国大部分地区,困扰着广大市民的生活,口罩市场出现热销,小明的爸爸用12000元购进甲、乙两种型号的口罩在自家商店销售,销售完后共获利2700元,进价和售价如表:
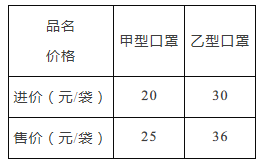
(1)小明爸爸的商店购进甲、乙两种型号口罩各多少袋?
(2)该商店第二次以原价购进甲、乙两种型号口罩,购进甲种型号口罩袋数不变,而购进乙种型号口罩袋数是第一次的2倍,甲种口罩按原售价出售,而效果更好的乙种口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋乙种型号的口罩最多打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
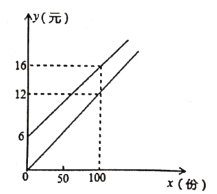
【题目】我校准备实行学案式教学,需印刷若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用![]() (元)与印刷份数
(元)与印刷份数![]() (份)之间的关系如图所式.
(份)之间的关系如图所式.
(1)求出甲、乙两种收费方式的函数关系式;
(2)我校八年级每次需印刷100-450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程![]() (米)与行驶时间
(米)与行驶时间![]() (分钟)的变化关系
(分钟)的变化关系
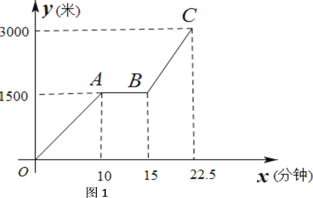
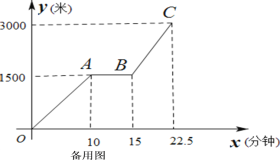
(1)求线段BC所表达的函数关系式;
(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;
(3)如果小贾的行驶速度是![]() 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面证明:

(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b.
证明:∵a⊥c (已知)
∴∠1= (垂直定义)
∵b∥c (已知)
∴∠1=∠2 ( )
∴∠2=∠1=90° ( )
∴a⊥b ( )
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE.
证明:∵AB∥CD (已知)
∴∠B= ( )
∵∠B+∠D=180° (已知)
∴∠C+∠D=180° ( )
∴CB∥DE ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组 ,有且仅有四个整数解,且使关于y的分式方程
,有且仅有四个整数解,且使关于y的分式方程![]() 有非负数解,则所有满足条件的整数a的值之和是________________.
有非负数解,则所有满足条件的整数a的值之和是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1,画出△A1B1C1.
(3)求(2)中C到C1经过的路径以及OB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P.
①求证:四边形CODP是菱形.
②若AD=6,AC=10,求四边形CODP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组 ![]() (a≥0),给出下列说法:
(a≥0),给出下列说法:
①当a=1时,方程组的解也是方程x+y=2的一个解;
②当x﹣2y>8时,a> ![]() ;
;
③不论a取什么实数,2x+y的值始终不变;
④某直角三角形的两条直角边长分别为x+y,x﹣y,则其面积最大值为 ![]() .
.
以上说法正确的是( )
A.②③
B.①②④
C.③④
D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com