
【题目】如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BDCE,求证:△ABD∽△ECA.
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:△ABD≌△BCE.
(2)求证:AC是线段ED的垂直平分线.
(3)△DBC是等腰三角形吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是( )
A.△BDF∽△BEC
B.△BFA∽△BEC
C.△BAC∽△BDA
D.△BDF∽△BAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49![]() ×(-5),看谁算的又快又对,有两位同学的解法如下:
×(-5),看谁算的又快又对,有两位同学的解法如下:
聪聪;原式=-![]() ×5=-
×5=-![]() -249
-249![]() ;
;
明明:原式=(49+![]() )×(-5)=49×(-5)+
)×(-5)=49×(-5)+![]() ×(-5)=-249
×(-5)=-249![]() ,
,
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:39![]() ×(-8).
×(-8).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
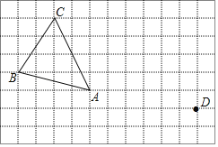
(1)△ABC的面积为______;
(2)请画出平移后的△DEF;
(3)利用格点画出△DEF的高FG(点G为垂足);
(4)若连接AD、CF,则这两条线段之间的关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
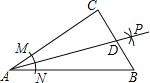
【题目】如图,在Rt△ABC中,∠C=90°,以A为圆心,以任意长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,以一个定长为半径画弧,两弧交于点P,作射线AP交BC于点D.若AC=8,BC=6,则CD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com