
【题目】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:△ABD≌△BCE.
(2)求证:AC是线段ED的垂直平分线.
(3)△DBC是等腰三角形吗?请说明理由.

【答案】(1)见解析;(2)见解析;(3)△DBC是等腰三角形,见解析.
【解析】
(1)如图,根据垂直关系可得∠1=∠2,再根据ASA即可证明△BAD≌△CBE;(2)由(1)得AD=AE,再求得∠6=∠7=45°,即可得证;(3)由垂直平分线的性质知CD=CE,由(1)得CE=BD,故△DBC是等腰三角形.
解:(1)如图证明:∵∠ABC=90°,BD⊥EC,
∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△BAD和△CBE中,
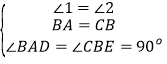 ,
,
∴△BAD≌△CBE(ASA),
(2)证明:∵E是AB中点,
∴EB=EA,
∵AD=BE,
∴AE=AD,
∵AD∥BC,
∴∠7=∠ACB=45°,
∵∠6=45°,
∴∠6=∠7,
又∵AD=AE,
∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形(CD=BD).
理由如下:
∵由(2)得:CD=CE,由(1)得:CE=BD,
∴CD=BD.
∴△DBC是等腰三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,以![]() 的边
的边![]() 、
、![]() 为边的等边三角
为边的等边三角![]() 和等边三角形
和等边三角形![]() ,四边形
,四边形![]() 是平行四边形.
是平行四边形.
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形;
是矩形;
![]() 当
当![]() 满足什么条件时,平行四边形
满足什么条件时,平行四边形![]() 不存在;
不存在;
![]() 当
当![]() 分别满足什么条件时,平行四边形
分别满足什么条件时,平行四边形![]() 是菱形,正方形?
是菱形,正方形?

查看答案和解析>>
科目:初中数学 来源: 题型:
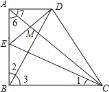
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
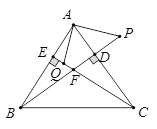
求证:(1)AP=AQ ;
(2)AP⊥AQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠C=90°,∠A=30°.
(1)尺规作图:作线段AB的垂直平分线l(保留作图痕迹,不写作法);
(2)在已作的图形中,若l分别交AB、AC及BC的延长线于点D、E、F,连接BE.求证:EF=2DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
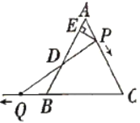
(1)若![]() 时,求
时,求![]() 的长;
的长;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生变化,请说明理由.
的长;如果发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com