
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
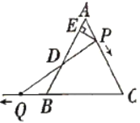
(1)若![]() 时,求
时,求![]() 的长;
的长;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生变化,请说明理由.
的长;如果发生变化,请说明理由.
【答案】(1)2(2)2(3)DE=3为定值,理由见解析
【解析】
(1)根据等边三角形的性质得到∠A=60![]() ,根据三角形内角和定理得到∠APE=30
,根据三角形内角和定理得到∠APE=30![]() ,根据直角三角形的性质计算;
,根据直角三角形的性质计算;
(2)过P作PF∥QC,证明△DBQ≌△DFP,根据全等三角形的性质计算即可;
(3)根据等边三角形的性质、直角三角形的性质解答.
(1)∵△ABC是等边三角形,
∴∠A=60![]() ,
,
∵PE⊥AB,
∴∠APE=30![]() ,
,
∵AE=1,∠APE=30![]() ,PE⊥AB,
,PE⊥AB,
∴AP=2AE=2;
(2)解:过P作PF∥QC,
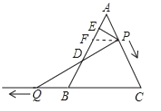
则△AFP是等边三角形,
∵P、Q同时出发,速度相同,即BQ=AP,
∴BQ=PF,
在△DBQ和△DFP中,
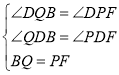 ,
,
∴△DBQ≌△DFP,
∴BD=DF,
∵∠BQD=∠BDQ=∠FDP=∠FPD=30![]() ,
,
∴BD=DF=FA=![]() AB=2,
AB=2,
∴AP=2;
(3)解:由(2)知BD=DF,
∵△AFP是等边三角形,PE⊥AB,
∴AE=EF,
∴DE=DF+EF=![]() BF+
BF+![]() FA=
FA=![]() AB=3为定值,即DE的长不变.
AB=3为定值,即DE的长不变.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:△ABD≌△BCE.
(2)求证:AC是线段ED的垂直平分线.
(3)△DBC是等腰三角形吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
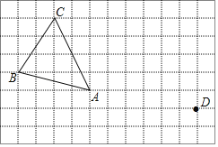
(1)△ABC的面积为______;
(2)请画出平移后的△DEF;
(3)利用格点画出△DEF的高FG(点G为垂足);
(4)若连接AD、CF,则这两条线段之间的关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在生活人们已经离不开密码,如取款、上网等都需要密码,有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式![]() ,因式分解的结果是
,因式分解的结果是![]() ,若取
,若取![]() ,
,![]() 时则各个因式的值是:
时则各个因式的值是:![]() ,
,![]() ,
,![]() ,把这些值从小到大排列得到
,把这些值从小到大排列得到![]() ,于是就可以把“018162”作为一个六位数的密码.对于多项式
,于是就可以把“018162”作为一个六位数的密码.对于多项式![]() ,取
,取![]() ,
,![]() 时,请你写出用上述方法产生的密码_________.
时,请你写出用上述方法产生的密码_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某著名景区依托天然河道新开发了一款乘船体验项目.小明乘船由甲地顺流而下到乙地,然后由乙地逆流而上到丙地,然后靠岸乘车离开景点.若水流速度为2km/小时,船在静水中的速度为8km/小时.在整个乘船过程中,轮船与甲地相距的路程S(千米)与轮船出发的时间t(小时)之间的关系如图所示,甲乙两地间的距离为_____千米.
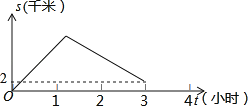
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以A为圆心,以任意长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,以一个定长为半径画弧,两弧交于点P,作射线AP交BC于点D.若AC=8,BC=6,则CD的长为( )
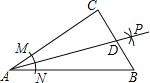
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为庆祝国庆节举办游园活动,小军来到摸球兑奖活动场地,李老师对小军说:“这里有甲、乙两个盒子,里面都装有一些乒乓球,你只能选择在其中一个盒子中摸球。”获奖规则如下:
甲盒中有白色乒乓球4个,黄色乒乓球1个,一人只能摸一次且一次摸出一个球,若这个球为黄色球,则可获得玩具熊一个,否则不得奖;
乙盒中有白色乒乓球2个,黄色乒乓球3个,一人只能摸一次且一次摸出两个球,若这两个球均为黄色球,则可获得玩具熊一个,否则不得奖;
请问小军在哪个盒子内摸球获得玩具熊的机会更大?请用概率知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设有足够多的黑白围棋子,摆成一个“中”字,下列图形中,第①个图形中有4 枚黑子和4枚白子,第②个图形中有6枚黑子和11枚白子,第③个图形中有8枚黑子和18枚白子,…,按此规律排列,则第⑧个图形中黑子和白子的枚数分别为( )
A.14和48
B.16和48
C.18和53
D.18和67
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com