
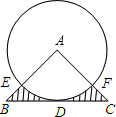
 如图,△ABC中,AB=6,AC=8,BC=10,以A为圆心的圆与BC相切于点D,与AB相交于点E,与AC交于点F,则阴影部分的面积S=24-$\frac{144π}{25}$.
如图,△ABC中,AB=6,AC=8,BC=10,以A为圆心的圆与BC相切于点D,与AB相交于点E,与AC交于点F,则阴影部分的面积S=24-$\frac{144π}{25}$. 分析 如图,作辅助线;首先证明∠A为直角,此为解决问题的关键性结论;运用三角形的面积公式求出AD;借助三角形、扇形的面积公式求出阴影部分的面积,即可解决问题.
解答 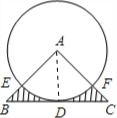 解:如图,连接AD;则AD⊥BC;
解:如图,连接AD;则AD⊥BC;
在△ABC中,∵62+82=102,
∴∠A=90°;
由三角形的面积公式得:
$\frac{1}{2}AB•AC=\frac{1}{2}BC•AD$,
即$\frac{1}{2}×6×8=\frac{1}{2}×10×AD$,
解得:AD=4.8,
∴S阴影=S△ABC-S扇形AEF
=$\frac{1}{2}×6×8$-$\frac{90π×4.{8}^{2}}{360}$
=24-$\frac{144π}{25}$,
故答案为24-$\frac{144π}{25}$.
点评 该题主要考查了勾股定理的逆定理、三角形的面积公式、扇形的面积公式等几何知识点及其应用问题;解题的方法是作辅助线,求出⊙A的半径;解题的关键是灵活运用勾股定理的逆定理、三角形的面积公式等来分析、判断、解答.


科目:初中数学 来源: 题型:选择题
 如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )| A. | (2,5) | B. | (2.5,5) | C. | (3,5) | D. | (3,6) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了了解本校七年级学生“双休日”在家的活动情况,对学生进行抽样调查,并将调查结果绘制成如图表:
某校为了了解本校七年级学生“双休日”在家的活动情况,对学生进行抽样调查,并将调查结果绘制成如图表:| 每日用在上网、看电视的时间 | 0~0.5(小时) | 1~2(小时) | 3~4(小时) | 5~6(小时) | 7小时以上 |
| 人数 | a | 26 | 14 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com