
【题目】如图,在直角坐标系中,抛物线y=ax2+2x+c过点A、B且与y轴交与点C(0,3),点P为抛物线对称轴x=l上一动点.
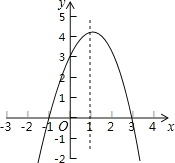
(1)求抛物线的解析式;
(2)求当AP+CP最小时点P的坐标.
【答案】(1)抛物线的解析式为y=﹣x2+2x+3;(2)P点坐标为(1,2).
【解析】
试题分析:(1)先把C(0,3)代入y=ax2+2x+c可求得c=3,再利用对称轴方程可求出a=﹣1,于是得到抛物线的解析式为y=﹣x2+2x+3;
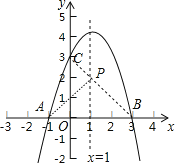
(2)利用抛物线与x轴的交点问题,通过解方程﹣x2+2x+3=0得到A(﹣1,0),B(3,0),连结BC交直线x=1于点P,如图,利用两点之间线段最短可判断此时PC+PA最小,利用待定系数法可计算出直线BC的解析式为y=﹣x+3,然后计算x=1的函数值即可得到P点坐标.
解:(1)把C(0,3)代入y=ax2+2x+c得c=3,
因为抛物线的对称轴为直线x=1,
所以﹣![]() =1,解得a=﹣1,
=1,解得a=﹣1,
所以抛物线的解析式为y=﹣x2+2x+3;
(2)当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=﹣3,则A(﹣1,0),B(3,0),
连结BC交直线x=1于点P,连接PA,如图,
∵PA=PB,
∴PA+PC=PC+PB=BC,
∴此时PC+PA最小,
设直线BC的解析式为y=kx+b,
把B(3,0),C(0,3)代入得![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=﹣x+3,
当x=1时,y=﹣x+3=2,
∴P点坐标为(1,2).


科目:初中数学 来源: 题型:
【题目】有一段导线,在0 ℃时电阻为2 Ω,温度每增加1 ℃,电阻增加0.008 Ω,那么电阻R(Ω)表示为温度t(℃)的函数关系式为( )
A. R=2+0.008 t B. R=2-0.008 t
C. t=2+0.008 R D. t=2-0.008 R
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
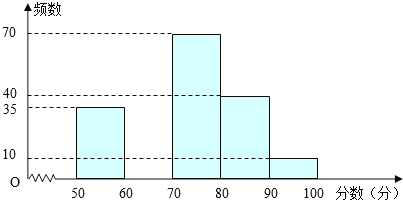
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,台球运动中,如果母球P击中边点A,经桌边反弹后击中相邻的另一桌边的点B,两次反弹.
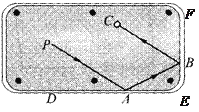
(1)若∠PAD=32度,求∠PAB的度数;
(2)母球P经过的路线BC与PA一定平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果△ABC∽△A′B′C′,BC=3,B′C′=1.8,则△A′B′C′与△ABC的相似比为( )
A.5:3
B.3:2
C.2:3
D.3:5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com