
【题目】在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数![]() 的图象上有且只有一个完美点
的图象上有且只有一个完美点![]() ,且当
,且当![]() 时,函数
时,函数![]() 的最小值为﹣3,最大值为1,则m的取值范围是( )
的最小值为﹣3,最大值为1,则m的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据完美点的概念令ax2+4x+c=x,即ax2+3x+c=0,由题意方程有两个相等的实数根,求得4ac=9,再根据方程的根为![]() =
=![]() ,从而求得a=-1,c=-
,从而求得a=-1,c=-![]() ,所以函数y=ax2+4x+c-
,所以函数y=ax2+4x+c-![]() =-x2+4x-3,根据函数解析式求得顶点坐标与纵坐标的交点坐标,根据y的取值,即可确定x的取值范围.
=-x2+4x-3,根据函数解析式求得顶点坐标与纵坐标的交点坐标,根据y的取值,即可确定x的取值范围.
解:令ax2+4x+c=x,即ax2+3x+c=0,
由题意,△=32-4ac=0,即4ac=9,
又方程的根为![]() =
=![]() ,
,
解得a=-1,c=-![]() ,
,
故函数y=ax2+4x+c-![]() =-x2+4x-3,
=-x2+4x-3,
如图,该函数图象顶点为(2,1),与y轴交点为(0,-3),由对称性,该函数图象也经过点(4,-3).
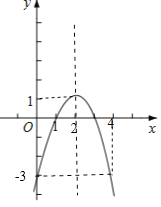
由于函数图象在对称轴x=2左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小,且当0≤x≤m时,函数y=-x2+4x-3的最小值为-3,最大值为1,
∴2≤m≤4,
故选:C.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在测量“河流宽度”的综合与实践活动中,小李同学设计的方案及测量数据如下:在河对岸边选定一个目标点A,在近岸取点B,C,D (点B,C,D在同一条直线上),AB⊥BD,∠ACB=45°,CD=20米,且.若测得∠ADB=25°,请你帮助小李求河的宽度AB.(sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,用篱笆靠墙围成矩形花围ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
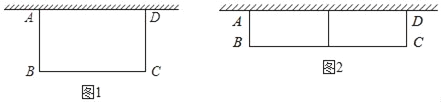
(1)若围成的花圃面积为40米2时,求BC的长;
(2)如图2若计划在花圃中间用一道隔成两个小矩形,且围成的花圃面积为50米2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
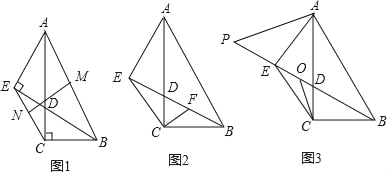
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=2BC,点D在边AC上,连接BD,过A作BD的垂线交BD的延长线于点E.
(1)若M,N分别为线段AB,EC的中点,如图1,求证:MN⊥EC;
(2)如图2,过点C作CF⊥EC交BD于点F,求证:AE=2BF;
(3)如图3,以AE为一边作一个角等于∠BAC,这个角的另一边与BE的延长线交于P点,O为BP的中点,连接OC,求证:OC=![]() (BE﹣PE).
(BE﹣PE).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.

(1)当BC=6时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次调查中,一共调查了 名学生;
(2)补全条形统计图;
(3)若该校共有1500名学生,估计爱好运动的学生有 人;
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ACD中,CD=1,AC=3.以AD为直径作⊙O,点C恰在圆上,点B为射线CD上一点,连接BA交⊙O于点E,连接CE交AD于点G,过点A作AF∥CD交DE的延长线于点F.
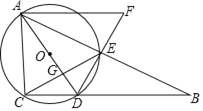
(1)若∠DAE=30°,求DE的长;
(2)求证:△AEC∽△FAD;
(3)当△GEA∽△FAD时,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1、图2、图3、…图n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动.
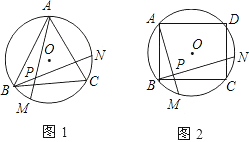
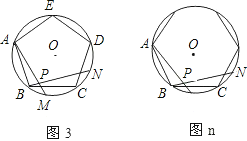
(1)求图1中∠APN的度数;
(2)求图2中,∠APN的度数,求图3中∠BPN的度数;
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com