
【题目】在△ACD中,CD=1,AC=3.以AD为直径作⊙O,点C恰在圆上,点B为射线CD上一点,连接BA交⊙O于点E,连接CE交AD于点G,过点A作AF∥CD交DE的延长线于点F.
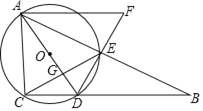
(1)若∠DAE=30°,求DE的长;
(2)求证:△AEC∽△FAD;
(3)当△GEA∽△FAD时,求DF的长.
【答案】(1)DE=![]() ;(2)见解析;(3)DF=
;(2)见解析;(3)DF=![]() .
.
【解析】
(1)先利用勾股定理求出AD,再用锐角三角函数即可得出结论;
(2)利用AF∥CD,得出∠ADC=∠FAD,进而得出∠AEC=∠FAD,即可得出结论;
(3)先用相似判断出∠EAG=∠ADF=45°,进而求出AE=![]() ,再判断出∠ACE=∠DCE,进而得出△AGH∽△DGC,求出AG,即可得出结论.
,再判断出∠ACE=∠DCE,进而得出△AGH∽△DGC,求出AG,即可得出结论.
解(1):∵点C以AD为直径的圆上,
∴∠ACD=90°,
根据勾股定理得,AD=![]() =
=![]() =
=![]() ,
,
∵点E以AD为直径的圆上,
∴∠AED=90°,
在Rt△ADE中,∠DAE=30°,
∴sin∠DAE=![]() ,
,
∴DE=ADsin∠DAE=![]() ×sin30°=
×sin30°=![]() ;
;
(2)∵AF∥CD,
∴∠ADC=∠FAD,
∵∠ADC=∠AEC,
∴∠AEC=∠FAD,
∵∠ACE=∠ADF,
∴△AEC∽△FAD;
(3)如图,
∵△GEA∽△FAD,
∴∠EAG=∠ADF,
∵∠AED=90°,
∴∠EAG=∠ADF=45°,
∴AE=![]() AD=
AD=![]() ×
×![]() =
=![]() ,
,
∵∠EAG=∠ADF,∠DCE=∠DAE,
∴∠DCE=∠ADE,
∵∠ADE=∠ACE,
∴∠ACE=∠DCE,
延长CE交AF的延长线于H,
∵AF∥CD,
∴∠H=∠DCE,
∴∠H=∠ACE,
∴AH=AC=3,
∵AF∥CD,
∴△AGH∽△DGC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AG=![]() ,
,
∵△GEA∽△FAD,
∴![]() ,
,
∴ ,
,
∴DF=![]() .
.



科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题:
(1)①方程x2-x-2 =0的解为__________
②方程x2-2x-3 =0的解为_______
③方程x2-3x-4 =0的解为_______
...
(2)根据以上方程特征及其解得特征,请猜想:
①方程x2-9x-10=0的解为_______
②请用配方法解方程x2-9x-10=0,以验证猜想结论的正确性。
(3)应用:关于x的方程______的解为x1 =-1,x2 =n+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为完美点.已知二次函数![]() 的图象上有且只有一个完美点
的图象上有且只有一个完美点![]() ,且当
,且当![]() 时,函数
时,函数![]() 的最小值为﹣3,最大值为1,则m的取值范围是( )
的最小值为﹣3,最大值为1,则m的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以AB为直径的半圆O交AC于点D,点E是
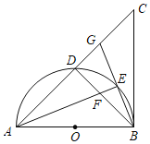
,以AB为直径的半圆O交AC于点D,点E是![]() 上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
(1)求证:![]() ;
;
(2)填空:
①若![]() ,且点E是
,且点E是![]() 的中点,则DF的长为 ;
的中点,则DF的长为 ;
②取![]() 的中点H,当
的中点H,当![]() 的度数为 时,四边形OBEH为菱形.
的度数为 时,四边形OBEH为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx+c与轴交于点A和点B,与y轴交于点C,作直线BC,点B的坐标为(6,0),点C的坐标为(0,﹣6).
x2+bx+c与轴交于点A和点B,与y轴交于点C,作直线BC,点B的坐标为(6,0),点C的坐标为(0,﹣6).

(1)求抛物线的解析式并写出其对称轴;
(2)D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求D点坐标;
(3)若E为y轴上且位于点C下方的一点,P为直线BC上的一点,在第四象限的抛物线上是否存在一点Q.使以C,E,P,Q为顶点的四边形是菱形?若存在,请求出Q点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
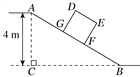
【题目】如图,某仓储中心有一斜坡AB,其坡比为i=1∶2,顶部A处的高AC为4 m,B,C在同一水平面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方形货柜的侧面图,其中DE=2.5 m,EF=2 m.将货柜沿斜坡向上运送,当BF=3.5 m时,求点D离地面的高.(![]() ≈2.236,结果精确到0.1 m)
≈2.236,结果精确到0.1 m)
查看答案和解析>>
科目:初中数学 来源: 题型:
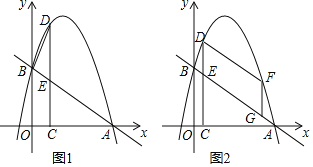
【题目】如图1,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
(1)求抛物线的函数表达式
(2)是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;
(3)如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | 27 |
C | 10000<x≤15000 | m |
D | 15000<x≤20000 | 33 |
E | x>20000 | 30 |
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有 户,表中m= ;
(2)请说明本次调查数据的中位数落在哪一组?
(3)在扇形统计图中,D组所在扇形的圆心角为多少度?
(4)这个社区有2500户家庭,请你估计年文化教育消费在10000元以上的家庭有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画出二次函数![]() 的图象.
的图象.
(1)利用图象求方程![]() 的近似很(结渠精确到
的近似很(结渠精确到![]() );
);
(2)设该抛物线的顶点为M,它与直线y=-3的两个交点分别为C、D,求△MCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com