
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃН![]() x2+bx+cгыжсНЛгкЕуAКЭЕуBЃЌгыyжсНЛгкЕуCЃЌзїжБЯпBCЃЌЕуBЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЌЕуCЕФзјБъЮЊЃЈ0ЃЌЉ6ЃЉЃЎ
x2+bx+cгыжсНЛгкЕуAКЭЕуBЃЌгыyжсНЛгкЕуCЃЌзїжБЯпBCЃЌЕуBЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЌЕуCЕФзјБъЮЊЃЈ0ЃЌЉ6ЃЉЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНВЂаДГіЦфЖдГЦжсЃЛ
ЃЈ2ЃЉDЮЊХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌЕБЁїBCDЪЧвдBCЮЊжБНЧБпЕФжБНЧШ§НЧаЮЪБЃЌЧѓDЕузјБъЃЛ
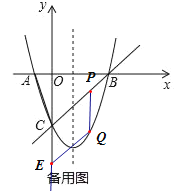
ЃЈ3ЃЉШєEЮЊyжсЩЯЧвЮЛгкЕуCЯТЗНЕФвЛЕуЃЌPЮЊжБЯпBCЩЯЕФвЛЕуЃЌдкЕкЫФЯѓЯоЕФХзЮяЯпЩЯЪЧЗёДцдквЛЕуQЃЎЪЙвдCЃЌEЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧыЧѓГіQЕуЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉКЏЪ§ЕФЖдГЦжсxЃН2ЃЛЃЈ2ЃЉDЃЈ2ЃЌЉ8ЃЉЛђЃЈ2ЃЌ4ЃЉЃЛЃЈ3ЃЉДцдкЃЌQЃЈ6Љ2![]() ЃЌ4Љ8
ЃЌ4Љ8![]() ЃЉЛђЃЈ2ЃЌЉ8ЃЉЃЎ
ЃЉЛђЃЈ2ЃЌЉ8ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуBЁЂCЕФзјБъДњШыЖўДЮКЏЪ§БэДяЪНЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЗжЁЯBCD=90ЁуЁЂЁЯDBC=90ЁуСНжжЧщПіЃЌЗжБ№ЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЗжCEЮЊСтаЮЕФвЛЬѕБпЁЂCEЮЊСтаЮЕФЖдНЧЯпСНжжЧщПіЃЌЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉНЋЕуBЁЂCЕФзјБъДњШыЖўДЮКЏЪ§БэДяЪНЕУЃК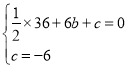 ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЙЪХзЮяЯпЕФБэДяЪНЮЊЃКyЃН![]() x2Љ2xЉ6ЃЌ
x2Љ2xЉ6ЃЌ
СюyЃН0ЃЌдђxЃНЉ2Лђ6ЃЌдђЕуAЃЈЉ2ЃЌ0ЃЉЃЌ
дђКЏЪ§ЕФЖдГЦжсxЃН2ЃЛ
ЃЈ2ЃЉЂйЕБЁЯBCDЃН90ЁуЪБЃЌ
НЋЕуBЁЂCЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНЕУЃК
жБЯпBCЕФБэДяЪНЮЊЃКyЃНxЉ6ЃЌ
дђжБЯпCDЕФБэДяЪНЮЊЃКyЃНЉxЉ6ЃЌ
ЕБxЃН2ЪБЃЌyЃНЉ8ЃЌЙЪЕуDЃЈ2ЃЌЉ8ЃЉЃЛ
ЂкЕБЁЯDBCЃН90ЁуЪБЃЌ
ЭЌРэПЩЕУЕуDЃЈ2ЃЌ4ЃЉЃЌ
ЙЪЕуDЃЈ2ЃЌЉ8ЃЉЛђЃЈ2ЃЌ4ЃЉЃЛ
ЃЈ3ЃЉЂйЕБCEЮЊСтаЮЕФвЛЬѕБпЪБЃЌ
дђPQЁЮCEЃЌЩшЕуPЃЈmЃЌmЉ6ЃЉЃЌдђЕуQЃЈmЃЌnЃЉЃЌ
дђnЃН![]() m2Љ2mЉ6ЁЂйЃЌ
m2Љ2mЉ6ЁЂйЃЌ
гЩЬтвтЕУЃКCPЃНPQЃЌ
МД![]() mЃНmЉ6ЉnЁЂкЃЌ
mЃНmЉ6ЉnЁЂкЃЌ
СЊСЂЂйЂкВЂНтЕУЃКmЃН6Љ2![]() ЃЌnЃН4Љ8
ЃЌnЃН4Љ8![]() ЃЌ
ЃЌ
дђЕуQЃЈ6Љ2![]() ЃЌ4Љ8
ЃЌ4Љ8![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЕБCEЮЊСтаЮЕФЖдНЧЯпЪБЃЌ
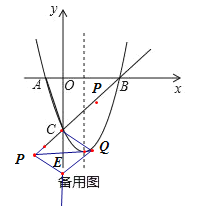
дђPQЁЭCEЃЌМДPQЁЮxжсЃЌ
ЩшЕуPЃЈmЃЌmЉ6ЃЉЃЌдђЕуQЃЈsЃЌmЉ6ЃЉЃЌ
ЦфжаmЉ6ЃН![]() s2Љ2sЉ6ЁЂлЃЌ
s2Љ2sЉ6ЁЂлЃЌ
дђPCЃНЉ![]() mЃЌ
mЃЌ
CQ2ЃНs2+m2ЃЌ
гЩЬтвтЕУЃКCQЃНCPЃЌ
МДЃКЃЈЉ![]() mЃЉ2ЃНs2+m2ЁЂмЃЌ
mЃЉ2ЃНs2+m2ЁЂмЃЌ
СЊСЂЂлЂмВЂНтЕУЃКmЃН6ЛђЉ2ЃЈЩсШЅ6ЃЉЃЌ
ЙЪЕуЃЈ2ЃЌЉ8ЃЉЃЛ
злЩЯЃЌЕуQЃЈ6Љ2![]() ЃЌ4Љ8
ЃЌ4Љ8![]() ЃЉЛђЃЈ2ЃЌЉ8ЃЉЃЎ
ЃЉЛђЃЈ2ЃЌЉ8ЃЉЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЁбOжа,ЕуCЪЧгХЛЁACBЕФжаЕу,DЁЂEЗжБ№ЪЧOAЁЂOBЩЯЕФЕу,ЧвAD=BE,ЯвCMЁЂCNЗжБ№Й§ЕуDЁЂE.
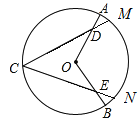
(1)ЧѓжЄЃКCD=CEЃЎ
(2)ЧѓжЄЃК![]() =
=![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкАыОЖЮЊ5ЕФЩШаЮAOBжаЃЌЁЯAOB=90ЁуЃЌЕуCЪЧЛЁABЩЯЕФвЛИіЖЏЕуЃЈВЛгыЕуAЁЂBжиКЯЃЉODЁЭBCЃЌOEЁЭACЃЌДЙзуЗжБ№ЮЊDЁЂEЃЎ

ЃЈ1ЃЉЕБBC=6ЪБЃЌЧѓЯпЖЮODЕФГЄЃЛ
ЃЈ2ЃЉдкЁїDOEжаЪЧЗёДцдкГЄЖШБЃГжВЛБфЕФБпЃПШчЙћДцдкЃЌЧыжИГіВЂЧѓЦфГЄЖШЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїВЮМгФГИіжЧСІОКД№НкФПЃЌД№ЖдзюКѓСНЕРЕЅбЁЬтОЭЫГРћЭЈЙиЃЎЕквЛЕРЕЅбЁЬтга3ИібЁЯюЃЌЕкЖўЕРЕЅбЁЬтга4ИібЁЯюЃЌетСНЕРЬтаЁУїЖМВЛЛсЃЌВЛЙ§аЁУїЛЙгавЛИіЁАЧѓжњЁБУЛгагУЃЈЪЙгУЁАЧѓжњЁБПЩвдШУжїГжШЫШЅЕєЦфжавЛЬтЕФвЛИіДэЮѓбЁЯюЃЉЃЎ
ЃЈ1ЃЉШчЙћаЁУїЕквЛЬтВЛЪЙгУЁАЧѓжњЁБЃЌФЧУДаЁУїД№ЖдЕквЛЕРЬтЕФИХТЪЪЧЁЁЁЁЃЎ
ЃЈ2ЃЉШчЙћаЁУїНЋЁАЧѓжњЁБСєдкЕкЖўЬтЪЙгУЃЌЧыгУЪїзДЭМЛђепСаБэРДЗжЮіаЁУїЫГРћЭЈЙиЕФИХТЪЃЎ
ЃЈ3ЃЉДгИХТЪЕФНЧЖШЗжЮіЃЌФуНЈвщаЁУїдкЕкМИЬтЪЙгУЁАЧѓжњЁБЃЎЃЈжБНгаДГіД№АИЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСвдЯТВФСЯЃЌВЂАДвЊЧѓЭъГЩЯргІЕФШЮЮёЃЎШчЭМЃЈ1ЃЉЃЌвбжЊЫФБпаЮABCDЕФЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌЕуMЪЧBCБпЕФжаЕуЃЌЙ§ЕуMзїMEЁЮACНЛBDгкЕуEЃЌзїMFЁЮBDНЛACгкЕуFЃЎЮвУЧГЦЫФБпаЮ0EMFЮЊЫФБпаЮABCDЕФЁААщЫцЫФБпаЮЁБЃЎ
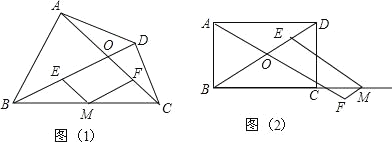
ЃЈ1ЃЉШєЫФБпаЮABCDЪЧСтаЮЃЌдђЦфЁААщЫцЫФБпаЮЁБЪЧЁЁ ЁЁЃЌШєЫФБпаЮABCDОиаЮЃЌдђЦфЁААщЫцЫФБпаЮЁБЪЧЃКЁЁ ЁЁЃЈдкКсЯпЩЯЬюЬиЪтЦНааЫФБпаЮЕФУћГЦЃЉ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌШєЫФБпаЮABCDЪЧОиаЮЃЌMЪЧBCбгГЄЯпЩЯЕФвЛИіЖЏЕуЃЌЦфЫћЬѕМўВЛБфЃЌЕуFТфдкACЕФбгГЄЯпЩЯЃЌЧыаДГіЯпЖЮOBЁЂMEЃЌMFжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїACDжаЃЌCDЃН1ЃЌACЃН3ЃЎвдADЮЊжБОЖзїЁбOЃЌЕуCЧЁдкдВЩЯЃЌЕуBЮЊЩфЯпCDЩЯвЛЕуЃЌСЌНгBAНЛЁбOгкЕуEЃЌСЌНгCEНЛADгкЕуGЃЌЙ§ЕуAзїAFЁЮCDНЛDEЕФбгГЄЯпгкЕуFЃЎ
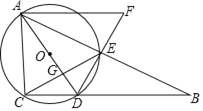
ЃЈ1ЃЉШєЁЯDAEЃН30ЁуЃЌЧѓDEЕФГЄЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїAECЁзЁїFADЃЛ
ЃЈ3ЃЉЕБЁїGEAЁзЁїFADЪБЃЌЧѓDFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЯьгІЁАбЇЯАЧПЙњЃЌдФЖСаЫСЩЁБЕФКХейЃЌФГаЃЙФРјбЇЩњРћгУПЮгрЪБМфЙуЗКдФЖСЃЌбЇаЃДђЫуЙКНјвЛХњЭМЪщЃЎЮЊСЫНтбЇЩњЖдЭМЪщРрБ№ЕФЯВЛЖЧщПіЃЌаЃбЇЩњЛсЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЌЙцЖЈБЛЕїВщбЇЩњДгЁАЮФбЇЁЂРњЪЗЁЂПЦбЇЁЂЩњЛюЁБжажЛбЁдёздМКзюЯВЛЖЕФвЛРрЃЌИљОнЕїВщНсЙћЛцжЦСЫЯТУцВЛЭъећЕФЭГМЦЭМЃЎ
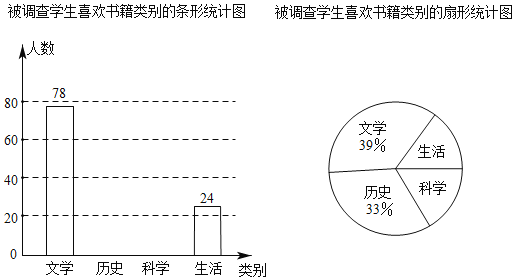
ЧыИљОнЭМБэаХЯЂЃЌНтД№ЯТСаЮЪЬтЃЎ
ЃЈ1ЃЉДЫДЮЙВЕїВщСЫбЇЩњЖрЩйШЫЃЛ
ЃЈ2ЃЉЧыЭЈЙ§МЦЫуВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУаЃЙВгабЇЩњ2200ШЫЃЌЧыЙРМЦетЫљбЇаЃЯВЛЖЁАПЦбЇЁБРрЪщЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЁЮCDЃЌEFгыABЃЌCDЗжБ№НЛгкЕуGЃЌHЃЌЁЯCHGЕФЦНЗжЯпHMНЛABгкЕуMЃЌШєЁЯEGBЃН50ЁуЃЌдђЁЯGMHЕФЖШЪ§ЮЊЃЈЁЁЁЁЃЉ

A. 50ЁуB. 55ЁуC. 60ЁуD. 65Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫдіНјЧззгЙиЯЕЃЌЗсИЛбЇЩњЕФЩњЛюЃЌбЇаЃОХФъМЖ(1)АрМвЮЏЛсзщжЏбЇЩњЁЂМвГЄвЛЦ№ВЮМгЛЇЭтЭиеЙЛюЖЏЃЌЫљСЊЯЕЕФТУааЩчЪеЗбБъзМШчЯТЃКШчЙћШЫЪ§ВЛГЌЙ§24ЃЌШЫОљЛюЖЏЗбгУЮЊ120дЊЃЛШчЙћШЫЪ§ГЌЙ§24ЃЌУПдіМг1ШЫЃЌШЫОљЛюЖЏЗбгУНЕЕЭ2дЊЃЌЕЋШЫОљЛюЖЏЗбгУВЛЕУЕЭгк85дЊЃЌЛюЖЏНсЪјКѓЃЌИУАрЙВжЇИЖИУТУааЩчЛюЖЏЗбгУ3 520дЊЃЌЧыЮЪИУАрЙВгаЖрЩйШЫВЮМгетДЮТУааЛюЖЏЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com