
【题目】为了响应“学习强国,阅读兴辽”的号召,某校鼓励学生利用课余时间广泛阅读,学校打算购进一批图书.为了解学生对图书类别的喜欢情况,校学生会随机抽取部分学生进行问卷调查,规定被调查学生从“文学、历史、科学、生活”中只选择自己最喜欢的一类,根据调查结果绘制了下面不完整的统计图.
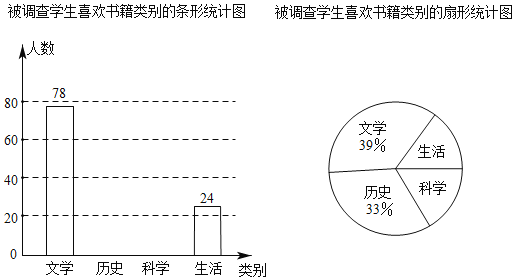
请根据图表信息,解答下列问题.
(1)此次共调查了学生多少人;
(2)请通过计算补全条形统计图;
(3)若该校共有学生2200人,请估计这所学校喜欢“科学”类书的学生人数.
【答案】(1)此次共调查了学生200人; (2)补全条形统计图如图所示,见解析;(3)该校2200名学生中喜欢“科学”类书的大约有352人.
【解析】
(1)从两个统计图中可得文学的人数为78人占调查人数的39%,可求调查人数;
(2)求出“历史”的人数,再求出“科学”的人数,即可补全条形统计图;
(3)样本估计总体,求出样本中“科学”占的百分比即为总体中“科学”所占比,从而可求出人数.
(1)78÷39%=200人
故答案为:200.
(2)200×33%=66人,200﹣78﹣66﹣24=32人,补全条形统计图如图所示:
(3)![]() 人,
人,
答:该校2200名学生中喜欢“科学”类书的大约有352人.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
A. 当a=1时,函数图象过点(-1,1)
B. 当a=-2时,函数图象与x轴没有交点
C. 若a>0,则当x≥1时,y随x的增大而减小
D. 若a<0,则当x≤1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了绿化小区,某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH.
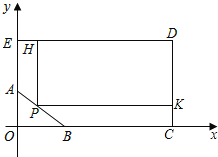
已知:![]() ,DE=100米,EA=60米,BC=70米,CD=80米.以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为O.
,DE=100米,EA=60米,BC=70米,CD=80米.以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为O.
(1)求直线AB的解析式.
(2)若设点P的横坐标为x,矩形PKDH的面积为S,求S关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx+c与轴交于点A和点B,与y轴交于点C,作直线BC,点B的坐标为(6,0),点C的坐标为(0,﹣6).
x2+bx+c与轴交于点A和点B,与y轴交于点C,作直线BC,点B的坐标为(6,0),点C的坐标为(0,﹣6).

(1)求抛物线的解析式并写出其对称轴;
(2)D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求D点坐标;
(3)若E为y轴上且位于点C下方的一点,P为直线BC上的一点,在第四象限的抛物线上是否存在一点Q.使以C,E,P,Q为顶点的四边形是菱形?若存在,请求出Q点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
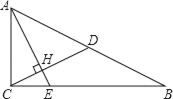
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
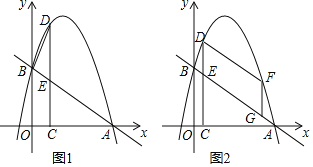
(1)求抛物线的函数表达式
(2)是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;
(3)如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.

(1)求抛物线的解析式.
(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD=2S△APQ时,求点P的坐标.
(3)如图2,G是线段OC上一个动点,连接DG,过点G作GM⊥DG交AC于点M,过点M作射线MN,使∠NMG=60°,交射线GD于点N;过点G作GH⊥MN,垂足为点H,连接BH.请直接写出线段BH的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在△ABC中,点D,E,F分别是边AB,BC,CA上的动点,若△DEF∽△ABC(点D、E、F的对应点分别为点A、B、C),则称△DEF是△ABC的子三角形,如图.
(1)已知:如图1,△ABC是等边三角形,点D,E,F分别是边AB,BC,CA上动点,且AD=BE=CF.
求证:△DEF是△ABC的子三角形.
(2)已知:如图2,△DEF是△ABC的子三角形,且AB=AC,∠A=90°,若BE=![]() ,求CF和AD的长.
,求CF和AD的长.
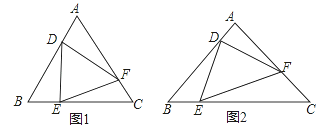
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com