
【题目】在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.

(1)求抛物线的解析式.
(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD=2S△APQ时,求点P的坐标.
(3)如图2,G是线段OC上一个动点,连接DG,过点G作GM⊥DG交AC于点M,过点M作射线MN,使∠NMG=60°,交射线GD于点N;过点G作GH⊥MN,垂足为点H,连接BH.请直接写出线段BH的最小值.
【答案】(1)y=﹣x2+3x+4;(2)点P的坐标为(1+![]() ,4+
,4+![]() )或(1﹣
)或(1﹣![]() ,4﹣
,4﹣![]() );(3)BH最小=
);(3)BH最小=![]() .
.
【解析】
(1)利用待定系数法求解可得;
(2)作PE∥x轴,交AB于点E,由![]() 且△AQD与△APQ是等高的两个三角形知
且△AQD与△APQ是等高的两个三角形知![]() ,证△PQE∽△DQB得
,证△PQE∽△DQB得![]() ,据此求得PE=2,求得直线AB的解析式为y=x+1,设E(x,x+1),知P(x-2,x+1),将点P坐标代入
,据此求得PE=2,求得直线AB的解析式为y=x+1,设E(x,x+1),知P(x-2,x+1),将点P坐标代入![]() 求得x的值,从而得出答案;
求得x的值,从而得出答案;
(3)证∠GHM=90°,再证点C、G、H、M共圆得∠GCH=∠GMH=60°,据此知点H在与y轴夹角为60°的定直线上,从而得BH⊥CH时,BH最小,作HP⊥x轴,并延长PH交AC于点Q,证∠BHP=∠HCM=30°,设OP=a,知CQ=a,从而得QH=![]() ,BP=1+a,在Rt△BPH中,得出HP=
,BP=1+a,在Rt△BPH中,得出HP=![]() (a+1),BH=2(1+a),根据QH+HP=AD=4可求得a的值,从而得出答案.
(a+1),BH=2(1+a),根据QH+HP=AD=4可求得a的值,从而得出答案.
(1)将点A(3,4),B(﹣1,0)代入y=ax2+bx+4,
得:![]() ,
,
解得![]() ,
,
∴y=﹣x2+3x+4;
(2)如图1,过点P作PE∥x轴,交AB于点E,
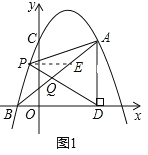
∵A(3,4),AD⊥x轴,
∴D(3,0),
∵B(﹣1,0),
∴BD=3﹣(﹣1)=4,
∵S△AQD=2S△APQ,△AQD与△APQ是等高的两个三角形,
∴![]() ,
,
∵PE∥x轴,
∴△PQE∽△DQB,
∴![]() ,
,
∴![]() ,
,
∴PE=2,
∴可求得直线AB的解析式为y=x+1,
设E(x,x+1),则P(x﹣2,x+1),
将点P坐标代入y=﹣x2+3x+4,得:﹣(x-2)2+3(x-2)+4=x+1,
解得x1=3+![]() ,x2=3﹣
,x2=3﹣![]() ,
,
当x=3+![]() 时,x﹣2=3+
时,x﹣2=3+![]() ﹣2=1+
﹣2=1+![]() ,x+1=3+
,x+1=3+![]() +1=4+
+1=4+![]() ,
,
∴点P(1+![]() ,4+
,4+![]() );
);
当x=3﹣![]() 时,x﹣2=3﹣
时,x﹣2=3﹣![]() ﹣2=1﹣
﹣2=1﹣![]() ,x+1=3﹣
,x+1=3﹣![]() +1=4﹣
+1=4﹣![]() ,
,
∴P(1﹣![]() ,4﹣
,4﹣![]() ),
),
∵点P是直线AB上方抛物线上的一个动点,
∴﹣1<x﹣2<3,
∴点P的坐标为(1+![]() ,4+
,4+![]() )或(1﹣
)或(1﹣![]() ,4﹣
,4﹣![]() );
);
(3)由(1)得,抛物线的解析式为y=﹣x2+3x+4,
∴C(0,4),
∵A(3,4),
∴AC∥x轴,
∴∠OCA=90°,
∴GH⊥MN,
∴∠GHM=90°,
在四边形CGHM中,∠GCM+∠GHM=180°,
∴点C、G、H、M共圆,
如图2,连接CH,
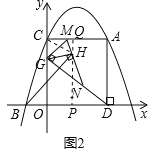
则∠GCH=∠GMH=60°,
∴点H在与y轴夹角为60°的定直线上,
∴当BH⊥CH时,BH最小,过点H作HP⊥x轴于点P,并延长PH交AC于点Q,
∵∠GCH=60°,
∴∠HCM=30°,
又BH⊥CH,
∴∠BHC=90°,
∴∠BHP=∠HCM=30°,
设OP=a,则CQ=a,
∴QH=![]() a,
a,
∵B(﹣1,0),
∴OB=1,
∴BP=1+a,
在Rt△BPH中,HP=![]() =
=![]() (a+1),BH=
(a+1),BH=![]() =2(1+a),
=2(1+a),
∵QH+HP=AD=4,
∴![]() a+
a+![]() (a+1)=4,
(a+1)=4,
解得a=![]() ,
,
∴BH最小=2(1+a)=![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.

(1)当BC=6时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“学习强国,阅读兴辽”的号召,某校鼓励学生利用课余时间广泛阅读,学校打算购进一批图书.为了解学生对图书类别的喜欢情况,校学生会随机抽取部分学生进行问卷调查,规定被调查学生从“文学、历史、科学、生活”中只选择自己最喜欢的一类,根据调查结果绘制了下面不完整的统计图.
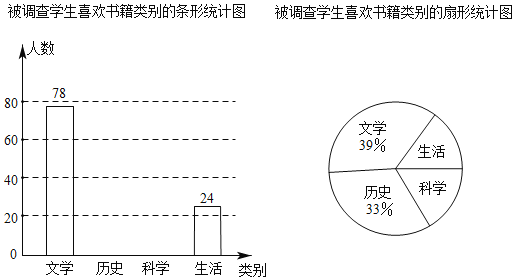
请根据图表信息,解答下列问题.
(1)此次共调查了学生多少人;
(2)请通过计算补全条形统计图;
(3)若该校共有学生2200人,请估计这所学校喜欢“科学”类书的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )

A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=![]() (k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
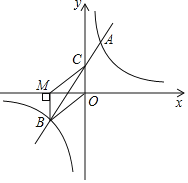
(1)求反比例函数和一次函数的解析式.
(2)连接OB,MC,求四边形MBOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1、图2、图3、…图n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动.
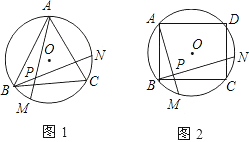
(1)求图1中∠APN的度数;
(2)求图2中,∠APN的度数,求图3中∠BPN的度数;
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点A在第四象限y1=﹣![]() 的图象上,点B在第一象限y2=
的图象上,点B在第一象限y2=![]() 的图象上,AB交x轴于点E,点C与点D在y轴上,AD=
的图象上,AB交x轴于点E,点C与点D在y轴上,AD=![]() ,S矩形OCBE=
,S矩形OCBE=![]() S矩形ODAE.
S矩形ODAE.
(1)求点B的坐标.
(2)若点P在x轴上,S△BPE=3,求直线BP的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增进亲子关系,丰富学生的生活,学校九年级(1)班家委会组织学生、家长一起参加户外拓展活动,所联系的旅行社收费标准如下:如果人数不超过24,人均活动费用为120元;如果人数超过24,每增加1人,人均活动费用降低2元,但人均活动费用不得低于85元,活动结束后,该班共支付该旅行社活动费用3 520元,请问该班共有多少人参加这次旅行活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
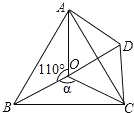
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com