
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=![]() (k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
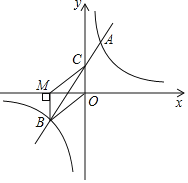
(1)求反比例函数和一次函数的解析式.
(2)连接OB,MC,求四边形MBOC的面积.
【答案】(1)y=![]() ,y=2x+2;(2)四边形MBOC的面积是4.
,y=2x+2;(2)四边形MBOC的面积是4.
【解析】
(1)根据题意可以求得点B的坐标,从而可以求得反比例函数的解析式,进而求得点A的坐标,从而可以求得一次函数的解析式;
(2)根据(1)中的函数解析式可以求得点C,从而可以求得四边形MBOC是平行四边形,根据面积公式即可求得.
解:(1)∵BM=OM=2,
∴点B的坐标为(﹣2,﹣2),
∵反比例函数y=![]() (k≠0)的图象经过点B,
(k≠0)的图象经过点B,
则﹣2=![]() ,得k=4,
,得k=4,
∴反比例函数的解析式为y=![]() ,
,
∵点A的纵坐标是4,
∴4=![]() ,得x=1,
,得x=1,
∴点A的坐标为(1,4),
∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(﹣2,﹣2),
∴![]() ,解得
,解得![]() ,
,
即一次函数的解析式为y=2x+2;
(2)∵y=2x+2与y轴交于点C,
∴点C的坐标为(0,2),
∵点B(﹣2,﹣2),点M(﹣2,0),
∴OC=MB=2,
∵BM⊥x轴,
∴MB∥OC,
∴四边形MBOC是平行四边形,
∴四边形MBOC的面积是:OMOC=4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】直线:![]() ,与
,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() :
:![]() ,经过点
,经过点![]() ,且与
,且与![]() 轴的另一个交点为点
轴的另一个交点为点![]() .
.

(1)若![]() ,求此时抛物线的解析式、顶点坐标及点
,求此时抛物线的解析式、顶点坐标及点![]() 坐标;
坐标;
(2)在直线![]() 与抛物线
与抛物线![]() 围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
(3)①直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标会变吗?说明理由;
的坐标会变吗?说明理由;
②若抛物线![]() 与直线
与直线![]() 在
在![]() 的范围内有唯一公共点,请直接写出
的范围内有唯一公共点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=![]() 或t=
或t=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. ①②③④B. ①②④
C. ①②D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小松想利用所学数学知识测量学校旗杆高度,如图,旗杆AB的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小松拿起绳子末端,后退至E处,并拉直绳子,此时绳子末端D距离地面2m且绳子与水平方向成45°角.求旗杆AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2,设剪去小正方形的边长为xcm,则可列方程为( )
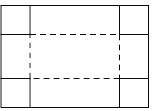
A.(30﹣2x)(40﹣x)=600B.(30﹣x)(40﹣x)=600
C.(30﹣x)(40﹣2x)=600D.(30﹣2x)(40﹣2x)=600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N分别在边AB,CD上,CN=1cm.现将四边形BCNM沿MN折叠,使点B,C分别落在点B',C'上.当点B'恰好落在边CD上时,线段BM的长为_____cm;在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为_____cm.
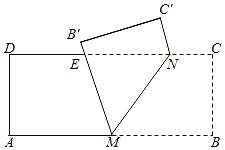
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com