
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,
上一点,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
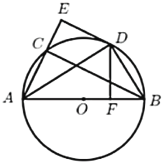
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,由等腰三角形的性质及角平分线的性质得出∠ADO=∠DAE,从而OD∥AE,由DE∥BC得∠E=90°,由两直线平行,同旁内角互补得出∠ODE=90°,由切线的判定定理得出答案;
(2)先由直径所对的圆周角是直角得出∠ADB=90°,再由OF=1,BF=2得出OB的值,进而得出AF和BA的值,然后证明△DBF∽△ABD,由相似三角形的性质得比例式,从而求得BD2的值,求算术平方根即可得出BD的值.
解:(1)连接OD,如图:
∵OA=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB,
∴∠DAE=∠OAD,
∴∠ADO=∠DAE,
∴OD∥AE,
∵DE∥BC,
∴∠E=90°,
∴∠ODE=180°∠E=90°,
∴DE是⊙O的切线;
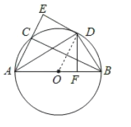
(2)因![]() 为直径,则
为直径,则![]()
∵![]() ,
,![]()
∴OB=3
∴![]() ,
,![]()
∵∠ADB=∠DFB=90°, ∠B=∠B
∴△DBF∽△ABD
∴![]()
∴![]()
所以![]() .
.


科目:初中数学 来源: 题型:
【题目】《中学生体质健康标准》规定的等级标准为:90分及以上为优秀,80~89分为良好,60~79分为及格,59分及以下为不及格.某校为了解七、八年级学生的体质健康情况,现从两年级中各随机抽取10名同学进行体质健康检测,并对成绩进行分析.成绩如下:
七年级 | 80 | 74 | 83 | 63 | 90 | 91 | 74 | 61 | 82 | 62 |
八年级 | 74 | 61 | 83 | 91 | 60 | 85 | 46 | 84 | 74 | 82 |
(1)根据上述数据,补充完成下列表格中序号.
整理数据:
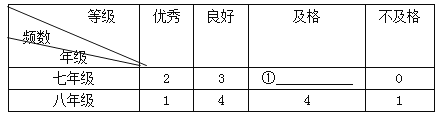
分析数据:
年级 | 平均数 | 众数 | 中位数 |
七年级 | ②_________ | 74 | 77 |
八年级 | 74 | 74 | ③____________ |
(2)该校目前七年级有300人,八年级有200人,试估计两个年级体质健康等级达到优秀的学生共有多少人?
(3)结合上述数据信息,你认为哪个年级学生的体质健康情况更好,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 直线
直线![]() 经过点
经过点![]() .
.
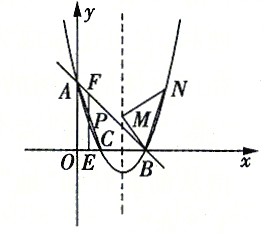
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方的抛物线上一动点,过点
下方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 设点
设点![]() 的横坐标为
的横坐标为![]() 若
若![]() 求
求![]() 的值;
的值;
(3)![]() 是第一象限对称轴右侧抛物线上的一点,连接
是第一象限对称轴右侧抛物线上的一点,连接![]() 抛物线的对称轴上是否存在点
抛物线的对称轴上是否存在点![]() .使得
.使得![]() 与
与![]() 相似,且
相似,且![]() 为直角,若存在,请直接写出点
为直角,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=![]() (k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
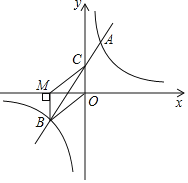
(1)求反比例函数和一次函数的解析式.
(2)连接OB,MC,求四边形MBOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
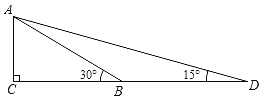
【题目】构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°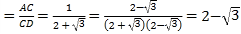 .类比这种方法,计算tan22.5°的值为( )
.类比这种方法,计算tan22.5°的值为( )
A.![]() B.
B.![]() ﹣1C.
﹣1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
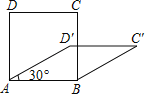
【题目】四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业承接了27000件产品的生产任务,计划安排甲、乙两个车间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.
(1)求甲、乙两个车间各有多少名工人参与生产?
(2)为了提前完成生产任务,该企业设计了两种方案:
方案一 甲车间租用先进生产设备,工人的工作效率可提高20%,乙车间维持不变.
方案二 乙车间再临时招聘若干名工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
①求乙车间需临时招聘的工人数;
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(性质探究)
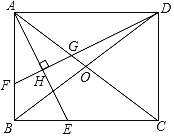
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.
(1)判断△AFG的形状并说明理由.
(2)求证:BF=2OG.
(迁移应用)
(3)记△DGO的面积为S1,△DBF的面积为S2,当![]() 时,求
时,求![]() 的值.
的值.
(拓展延伸)
(4)若DF交射线AB于点F,(性质探究)中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的![]() 时,请直接写出tan∠BAE的值.
时,请直接写出tan∠BAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
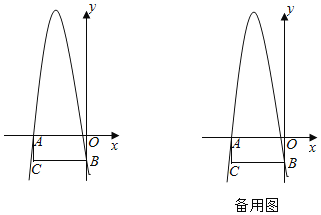
【题目】如图,在平面直角坐标系中,矩形AOBC的边AO在x轴的负半轴上,边OB在y轴的负半轴上.且AO=12,OB=9.抛物线y=﹣x2+bx+c经过点A和点B.
(1)求抛物线的表达式;
(2)在第二象限的抛物线上找一点M,连接AM,BM,AB,当△ABM面积最大时,求点M的坐标;
(3)点D是线段AO上的动点,点E是线段BO上的动点,点F是射线AC上的动点,连接EF,DF,DE,BD,且EF是线段BD的垂直平分线.当CF=1时.
①直接写出点D的坐标 ;
②若△DEF的面积为30,当抛物线y=﹣x2+bx+c经过平移同时过点D和点E时,请直接写出此时的抛物线的表达式 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com