
°ĺŐ‚ńŅ°Ņ£®–‘÷ ŐĹĺŅ£©
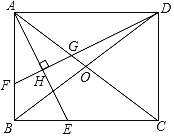
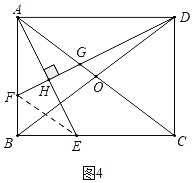
»ÁÕľ£¨‘ŕĺō–őABCD÷–£¨∂‘Ĺ«ŌŖAC£¨BDŌŗĹĽ”ŕĶ„O£¨AE∆Ĺ∑÷°ŌBAC£¨ĹĽBC”ŕĶ„E£ģ◊ųDF°ÕAE”ŕĶ„H£¨∑÷ĪūĹĽAB£¨AC”ŕĶ„F£¨G£ģ
£®1£©Ň–∂Ō°ųAFGĶń–ő◊ī≤ĘňĶ√ųņŪ”…£ģ
£®2£©«ů÷§£ļBF=2OG£ģ
£®«®“∆”¶”√£©
£®3£©ľ«°ųDGOĶń√śĽżő™S1£¨°ųDBFĶń√śĽżő™S2£¨ĶĪ![]() Ī£¨«ů
Ī£¨«ů![]() Ķń÷Ķ£ģ
Ķń÷Ķ£ģ
£®Õō’Ļ—”…ž£©
£®4£©»ŰDFĹĽ…šŌŖAB”ŕĶ„F£¨£®–‘÷ ŐĹĺŅ£©÷–Ķń∆š”ŗŐűľĢ≤ĽĪš£¨Ń¨ĹŠEF£¨ĶĪ°ųBEFĶń√śĽżő™ĺō–őABCD√śĽżĶń![]() Ī£¨«Ž÷ĪĹ”–ī≥Ųtan°ŌBAEĶń÷Ķ£ģ
Ī£¨«Ž÷ĪĹ”–ī≥Ųtan°ŌBAEĶń÷Ķ£ģ
°ĺīūįł°Ņ£®1£©Ķ»—Ł»żĹ«–ő£¨ņŪ”…ľŻĹ‚őŲ£Ľ£®2£©ľŻĹ‚őŲ£Ľ£®3£©![]() £Ľ£®4£©
£Ľ£®4£©![]() ĽÚ
ĽÚ![]()
°ĺĹ‚őŲ°Ņ
£®1£©»ÁÕľ1÷–£¨°ųAFG «Ķ»—Ł»żĹ«–ő£¨ņŻ”√»ęĶ»»żĹ«–őĶń–‘÷ ÷§√ųľīŅ…£ģ
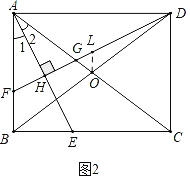
£®2£©»ÁÕľ2÷–£¨ĻżĶ„O◊ųOL°őABĹĽDF”ŕL£¨‘Ú°ŌAFG=°ŌOLG£ģ ◊Ō»÷§√ųOG=OL£¨‘Ŕ÷§√ųBF=2OLľīŅ…Ĺ‚ĺŲő Ő‚£ģ
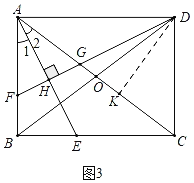
£®3£©»ÁÕľ3÷–£¨ĻżĶ„D◊ųDK°ÕAC”ŕK£¨‘Ú°ŌDKA=°ŌCDA=90°„£¨ņŻ”√Ōŗň∆»żĹ«–őĶń–‘÷ Ĺ‚ĺŲő Ő‚ľīŅ…£ģ
£®4£©…ŤOG=a£¨AG=k£ģ∑÷ŃĹ÷÷«ť–ő£ļĘŔ»ÁÕľ4÷–£¨Ń¨Ĺ”EF£¨ĶĪĶ„F‘ŕŌŖ∂őAB…Ō Ī£¨Ķ„G‘ŕOA…Ō£ģĘŕ»ÁÕľ5÷–£¨ĶĪĶ„F‘ŕABĶń—”≥§ŌŖ…Ō Ī£¨Ķ„G‘ŕŌŖ∂őOC…Ō£¨Ń¨Ĺ”EF£ģ∑÷Īū«ůĹ‚ľīŅ…Ĺ‚ĺŲő Ő‚£ģ
£®1£©Ĺ‚£ļ»ÁÕľ1÷–£¨°ųAFG «Ķ»—Ł»żĹ«–ő£ģ
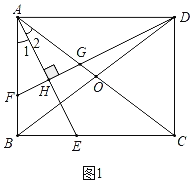
ņŪ”…£ļ°ŖAE∆Ĺ∑÷°ŌBAC£¨
°ŗ°Ō1=°Ō2£¨
°ŖDF°ÕAE£¨
°ŗ°ŌAHF=°ŌAHG=90°„£¨
°ŖAH=AH£¨
°ŗ°ųAHF°’°ųAHG£®ASA£©£¨
°ŗAF=AG£¨
°ŗ°ųAFG «Ķ»—Ł»żĹ«–ő£ģ
£®2£©÷§√ų£ļ»ÁÕľ2÷–£¨ĻżĶ„O◊ųOL°őABĹĽDF”ŕL£¨‘Ú°ŌAFG=°ŌOLG£ģ
°ŖAF=AG£¨
°ŗ°ŌAFG=°ŌAGF£¨
°Ŗ°ŌAGF=°ŌOGL£¨
°ŗ°ŌOGL=°ŌOLG£¨
°ŗOG=OL£¨
°ŖOL°őAB£¨
°ŗ°ųDLO°◊°ųDFB£¨
°ŗ![]() £¨
£¨
°ŖňńĪŖ–őABCD «ĺō–ő£¨
°ŗBD=2OD£¨
°ŗBF=2OL£¨
°ŗBF=2OG£ģ
£®3£©Ĺ‚£ļ»ÁÕľ3÷–£¨ĻżĶ„D◊ųDK°ÕAC”ŕK£¨‘Ú°ŌDKA=°ŌCDA=90°„£¨
°Ŗ°ŌDAK=°ŌCAD£¨
°ŗ°ųADK°◊°ųACD£¨
°ŗ![]() £¨
£¨
°ŖS1=![]() OGDK£¨S2=
OGDK£¨S2=![]() BFAD£¨
BFAD£¨
”÷°ŖBF=2OG£¨![]() £¨
£¨
°ŗ![]() £¨…ŤCD=2x£¨AC=3x£¨‘ÚAD=
£¨…ŤCD=2x£¨AC=3x£¨‘ÚAD= ![]() £¨
£¨
°ŗ![]() £ģ
£ģ
£®4£©Ĺ‚£ļ…ŤOG=a£¨AG=k£ģ
ĘŔ»ÁÕľ4÷–£¨Ń¨Ĺ”EF£¨ĶĪĶ„F‘ŕŌŖ∂őAB…Ō Ī£¨Ķ„G‘ŕOA…Ō£ģ
°ŖAF=AG£¨BF=2OG£¨
°ŗAF=AG=k£¨BF=2a£¨
°ŗAB=k+2a£¨AC=2£®k+a£©£¨
°ŗAD2=AC2©ĀCD2=[2£®k+a£©]2©Ā£®k+2a£©2=3k2+4ka£¨
°Ŗ°ŌABE=°ŌDAF=90°„£¨°ŌBAE=°ŌADF£¨
°ŗ°ųABE°◊°ųDAF£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
”…Ő‚“‚£ļ![]() =AD£®k+2a£©£¨
=AD£®k+2a£©£¨
°ŗAD2=10ka£¨
ľī10ka=3k2+4ka£¨
°ŗk=2a£¨
°ŗAD= ![]() £¨
£¨
°ŗBE= ![]() =
= ![]() £¨AB=4a£¨
£¨AB=4a£¨
°ŗtan°ŌBAE= ![]() £ģ
£ģ
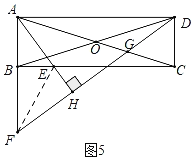
Ęŕ»ÁÕľ5÷–£¨ĶĪĶ„F‘ŕABĶń—”≥§ŌŖ…Ō Ī£¨Ķ„G‘ŕŌŖ∂őOC…Ō£¨Ń¨Ĺ”EF£ģ
°ŖAF=AG£¨BF=2OG£¨
°ŗAF=AG=k£¨BF=2a£¨
°ŗAB=k©Ā2a£¨AC=2£®k©Āa£©£¨
°ŗAD2=AC2©ĀCD2=[2£®k©Āa£©]2©Ā£®k©Ā2a£©2=3k2©Ā4ka£¨
°Ŗ°ŌABE=°ŌDAF=90°„£¨°ŌBAE=°ŌADF£¨
°ŗ°ųABE°◊°ųDAF£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ ![]() £¨
£¨
”…Ő‚“‚£ļ![]() =AD£®k©Ā2a£©£¨
=AD£®k©Ā2a£©£¨
°ŗAD2=10ka£¨
ľī10ka=3k2©Ā4ka£¨
°ŗk= ![]() £¨
£¨
°ŗAD= ![]() £¨
£¨
°ŗ![]() £¨AB=
£¨AB= ![]() £¨
£¨
°ŗtan°ŌBAE= ![]() £¨
£¨
◊Ř…Ōňý Ų£¨tan°ŌBAEĶń÷Ķő™![]() ĽÚ
ĽÚ![]() £ģ
£ģ


 ≤Ĺ≤ĹłŖīÔĪÍĺŪŌĶŃ–īūįł
≤Ĺ≤ĹłŖīÔĪÍĺŪŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥≥¨ –Ōķ Ř“Ľ÷÷…Ő∆∑£¨≥…Īĺ√Ņ«ßŅň40‘™£¨Ļś∂®√Ņ«ßŅň ŘľŘ≤ĽĶÕ”ŕ≥…Īĺ£¨«“≤ĽłŖ”ŕ80‘™£¨ĺ≠ –≥°Ķų≤ť£¨√ŅŐžĶńŌķ ŘŃŅy£®«ßŅň£©”Ž√Ņ«ßŅň ŘľŘx£®‘™£©¬ķ◊„“ĽīőļĮ żĻōŌĶ£¨≤Ņ∑÷ żĺ›»ÁŌ¬ĪŪ£ļ
ŘľŘx£®‘™/«ßŅň£© | 50 | 60 | 70 |
Ōķ ŘŃŅy£®«ßŅň£© | 100 | 80 | 60 |
£®1£©«ůy”Žx÷ģľšĶńļĮ żĪŪīÔ Ĺ£Ľ
£®2£©…Ť…Ő∆∑√ŅŐžĶń◊‹ņŻ»ůő™W£®‘™£©£¨‘ÚĶĪ ŘľŘx∂®ő™∂ŗ…Ŕ‘™ Ī£¨≥ß…Ő√ŅŐžń‹ĽŮĶ√◊ÓīůņŻ»ů£Ņ◊ÓīůņŻ»ů «∂ŗ…Ŕ£Ņ
£®3£©»ÁĻŻ≥¨ –“™ĽŮĶ√√ŅŐž≤ĽĶÕ”ŕ1350‘™ĶńņŻ»ů£¨«“∑ŻļŌ≥¨ –◊‘ľļĶńĻś∂®£¨ń«√īł√…Ő∆∑√Ņ«ßŅň ŘľŘĶń»°÷Ķ∑∂őß «∂ŗ…Ŕ£Ņ«ŽňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨![]() «
«![]() Ķń÷Īĺ∂£¨Ķ„
Ķń÷Īĺ∂£¨Ķ„![]() «
«![]() …Ō“ĽĶ„£¨
…Ō“ĽĶ„£¨![]() Ķń∆Ĺ∑÷ŌŖ
Ķń∆Ĺ∑÷ŌŖ![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨ĻżĶ„
£¨ĻżĶ„![]() ◊ų
◊ų![]() ĹĽ
ĹĽ![]() Ķń—”≥§ŌŖ”ŕĶ„
Ķń—”≥§ŌŖ”ŕĶ„![]() £ģ
£ģ
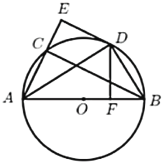
£®1£©«ů÷§£ļ![]() «
«![]() Ķń«–ŌŖ£Ľ
Ķń«–ŌŖ£Ľ
£®2£©ĻżĶ„![]() ◊ų
◊ų![]() ”ŕĶ„
”ŕĶ„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £ģ»Ű
£ģ»Ű![]() £¨
£¨![]() £¨«ů
£¨«ů![]() Ķń≥§∂»£ģ
Ķń≥§∂»£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
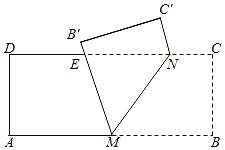
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨”–“Ľ’Ňĺō–ő÷ĹŐűABCD£¨AB£Ĺ5cm£¨BC£Ĺ2cm£¨Ķ„M£¨N∑÷Īū‘ŕĪŖAB£¨CD…Ō£¨CN£Ĺ1cm£ģŌ÷ĹęňńĪŖ–őBCNM—ōMN’ŘĶĢ£¨ ĻĶ„B£¨C∑÷Īū¬š‘ŕĶ„B'£¨C'…Ō£ģĶĪĶ„B'«°ļ√¬š‘ŕĪŖCD…Ō Ī£¨ŌŖ∂őBMĶń≥§ő™_____cm£Ľ‘ŕĶ„Mī”Ķ„A‘ň∂ĮĶĹĶ„BĶńĻż≥Ő÷–£¨»ŰĪŖMB'”ŽĪŖCDĹĽ”ŕĶ„E£¨‘ÚĶ„EŌŗ”¶‘ň∂ĮĶń¬∑ĺ∂≥§ő™_____cm£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
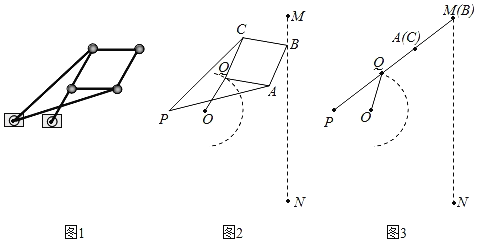
°ĺŐ‚ńŅ°ŅÕľ1 «”…∆ŖłýѨłňŃīĹ”∂Ý≥…ĶńĽķ–Ķ◊į÷√£¨Õľ2 «∆š ĺ“‚Õľ£ģ“—÷™O£¨PŃĹĶ„ĻŐ∂®£¨Ń¨łňPA=PC=140cm£¨AB=BC=CQ=QA=60cm£¨OQ=50cm£¨O£¨PŃĹĶ„ľšĺŗ”ŽOQ≥§∂»ŌŗĶ»£ģĶĪOQ»∆Ķ„O◊™∂Į Ī£¨Ķ„A£¨B£¨CĶńőĽ÷√ňś÷ģłńĪš£¨Ķ„B«°ļ√‘ŕŌŖ∂őMN…ŌņīĽō‘ň∂Į£ģĶĪĶ„B‘ň∂Į÷ŃĶ„MĽÚN Ī£¨Ķ„A£¨C÷ōļŌ£¨Ķ„P£¨Q£¨A£¨B‘ŕÕ¨“Ľ÷ĪŌŖ…Ō£®»ÁÕľ3£©£ģ
£®1£©Ķ„PĶĹMNĶńĺŗņŽő™_____cm£ģ
£®2£©ĶĪĶ„P£¨O£¨A‘ŕÕ¨“Ľ÷ĪŌŖ…Ō Ī£¨Ķ„QĶĹMNĶńĺŗņŽő™_____cm£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
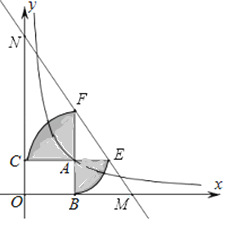
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™∂ĮĶ„A‘ŕļĮ ż![]() ĶńÕľŌů…Ō£¨AB°Õx÷Š”ŕĶ„B£¨AC°Õy÷Š”ŕĶ„C£¨—”≥§CAĹĽ“‘Aő™‘≤–ńAB≥§ő™įŽĺ∂Ķń‘≤Ľ°”ŕĶ„E£¨—”≥§BAĹĽ“‘Aő™‘≤–ńAC≥§ő™įŽĺ∂Ķń‘≤Ľ°”ŕĶ„F£¨÷ĪŌŖEF∑÷ĪūĹĽx÷Š°Ęy÷Š”ŕĶ„M°ĘN£¨ĶĪNF£Ĺ4EM Ī£¨Õľ÷–“ű”į≤Ņ∑÷Ķń√śĽżĶ»”ŕ_____£ģ
ĶńÕľŌů…Ō£¨AB°Õx÷Š”ŕĶ„B£¨AC°Õy÷Š”ŕĶ„C£¨—”≥§CAĹĽ“‘Aő™‘≤–ńAB≥§ő™įŽĺ∂Ķń‘≤Ľ°”ŕĶ„E£¨—”≥§BAĹĽ“‘Aő™‘≤–ńAC≥§ő™įŽĺ∂Ķń‘≤Ľ°”ŕĶ„F£¨÷ĪŌŖEF∑÷ĪūĹĽx÷Š°Ęy÷Š”ŕĶ„M°ĘN£¨ĶĪNF£Ĺ4EM Ī£¨Õľ÷–“ű”į≤Ņ∑÷Ķń√śĽżĶ»”ŕ_____£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨į—“Ľ’Ň≥§∑Ĺ–ő÷Ĺ∆¨![]() £¨—ō∂‘Ĺ«ŌŖ
£¨—ō∂‘Ĺ«ŌŖ![]() ’ŘĶĢ£¨Ķ„
’ŘĶĢ£¨Ķ„![]() Ķń∂‘”¶Ķ„ő™
Ķń∂‘”¶Ķ„ő™![]() £¨
£¨![]() ”Ž
”Ž![]() ŌŗĹĽ”ŕĶ„
ŌŗĹĽ”ŕĶ„![]() £¨‘ÚŌ¬Ń–ĹŠ¬Ř÷–≤Ľ“Ľ∂®’ż»∑Ķń «£® £©
£¨‘ÚŌ¬Ń–ĹŠ¬Ř÷–≤Ľ“Ľ∂®’ż»∑Ķń «£® £©

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨°ųABCńŕĹ””ŕ°—O£¨°ŌCBG=°ŌA£¨CDő™÷Īĺ∂£¨OC”ŽABŌŗĹĽ”ŕĶ„E£¨ĻżĶ„E◊ųEF°ÕBC£¨īĻ◊„ő™F£¨—”≥§CDĹĽGBĶń—”≥§ŌŖ”ŕĶ„P£¨Ń¨Ĺ”BD£ģ
£®1£©«ů÷§£ļPG”Ž°—OŌŗ«–£Ľ
£®2£©»Ű![]() =
=![]() £¨«ů
£¨«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨»Ű°—OĶńįŽĺ∂ő™8£¨PD=OD£¨«ůOEĶń≥§£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
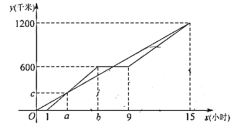
°ĺŐ‚ńŅ°Ņľ◊°Ę““ŃĹ≥Ķ—ōÕ¨“ĽŐűĶņ¬∑ī”![]() Ķō≥Ų∑ĘŌÚ1200
Ķō≥Ų∑ĘŌÚ1200![]() Õ‚Ķń
Õ‚Ķń![]() Ķō šňÕĹŰľĪőÔ◊ £¨ľ◊‘ŕÕĺ÷––›ŌĘŃň3–° Ī£¨–›ŌĘ«įļůĶńňŔ∂»≤ĽÕ¨£¨◊ÓļůŃĹ≥ĶÕ¨ ĪĶĹīÔ
Ķō šňÕĹŰľĪőÔ◊ £¨ľ◊‘ŕÕĺ÷––›ŌĘŃň3–° Ī£¨–›ŌĘ«įļůĶńňŔ∂»≤ĽÕ¨£¨◊ÓļůŃĹ≥ĶÕ¨ ĪĶĹīÔ![]() Ķō£¨»ÁÕľľ◊°Ę““ŃĹ≥ĶĶĹ
Ķō£¨»ÁÕľľ◊°Ę““ŃĹ≥ĶĶĹ![]() ĶōĶńĺŗņŽ
ĶōĶńĺŗņŽ![]() £®«ß√◊£©”Ž““≥Ķ–– Ľ Īľš
£®«ß√◊£©”Ž““≥Ķ–– Ľ Īľš![]() £®–° Ī£©÷ģľšĶńļĮ żÕľŌů£ģ
£®–° Ī£©÷ģľšĶńļĮ żÕľŌů£ģ
£®1£©ľ◊≥Ķ–›ŌĘ«įĶń–– ĽňŔ∂»ő™ «ß√◊/ Ī£¨““≥ĶĶńňŔ∂»ő™ «ß√◊/ Ī£Ľ
£®2£©ĶĪ9°‹![]() °‹15£¨«ůľ◊≥ĶĶń–– Ľ¬∑≥Ő
°‹15£¨«ůľ◊≥ĶĶń–– Ľ¬∑≥Ő![]() ”Ž
”Ž![]() ÷ģľšĶńļĮ żĻōŌĶ Ĺ£Ľ
÷ģľšĶńļĮ żĻōŌĶ Ĺ£Ľ
£®3£©÷ĪĹ”–ī≥Ųľ◊≥Ų∑Ę∂ŗ≥§ Īľš”Ž““‘ŕÕĺ÷–Ōŗ”Ų£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com