
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
���𰸡���1��y����2x+200 ��40��x��80������2���ۼ�Ϊ70Ԫʱ�������������������1800Ԫ����3��55��x��80�����ɼ�����
��������
��1������ϵ�������ɵã�
��2��������������ÿǧ�����������������ɵú�������ʽ�������䷽�ɶ���ʽ���ɵ���ֵ�����
��3�����W��1350ʱx��ֵ���ٸ��ݶ��κ������������W��1350ʱx��ȡֵ��Χ���̶�������ÿǧ���ۼ۲����ڳɱ��Ҳ�����80Ԫ���ó��𰸣�
��1����y��kx+b��
����50��100������60��80�����룬�ã�
![]() ��
��
��ã�![]() ��
��
��y����2x+200 ��40��x��80����
��2��W����x��40������2x+200��
����2x2+280x��8000
����2��x��70��2+1800��
�൱x��70ʱ��Wȡ�����ֵΪ1800��
���ۼ�Ϊ70Ԫʱ�������������������1800Ԫ��
��3����W��1350ʱ���ã���2x2+280x��8000��1350��
��ã�x��55��x��85��
�߸������ߵĿ������£�
���Ե�55��x��85ʱ��W��1350��
�֡�ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ����40��x��80��
�����Ʒÿǧ���ۼ۵�ȡֵ��Χ��55��x��80��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʯ���ڴ������Ҽ��������������У��̻����β���������ijУ�ƻ�����A��B������ľ��100�ý���У�̻����������г����飺����A����ľ2�ã�B����ľ5�ã�����600Ԫ������A����ľ3�ã�B����ľ1�ã�����380Ԫ��
��1����A�֣�B����ľÿ�ø�����Ԫ��
��2������Ҫ������A����ľ������������B����ľ������3����ѧУ���б깫˾ǩ���ĺ�ͬ�й涨�����г��۸������£��������������أ���ʵ�ʸ����ܽ��г��۾����Żݣ������һ�ֹ�����ľ�ķ�����ʹʵ������������ʡ���������ʡ�ķ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
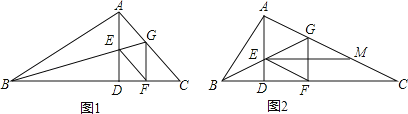
����Ŀ���ڡ�ABC�У���BAC��90�㣬AD��BC��D��BGƽ�֡�ABC��AD��E����AC��G��GF��BC��F������EF��
��1����ͼ1����֤���ı���AEFG�����Σ�
��2����ͼ2����EΪBG���е㣬����E��EM��BC��AC��M���ڲ������κθ����ߵ�����£���ֱ��д��ͼ2����CM��![]() ���������߶Σ�
���������߶Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��¥�Ķ�������һ������CD��С����ɽ�µ��½�A����ù���Ƶײ�D������Ϊ60����������AB�����ߵ�B����ù���ƶ���C������Ϊ45������֪ɽ��AB���¶�i=1��![]() ��AB=10����AE=15������i=1��
��AB=10����AE=15������i=1��![]() ��ָ�����Ǧֱ�߶�BH��ˮƽ����AH�ıȣ�
��ָ�����Ǧֱ�߶�BH��ˮƽ����AH�ıȣ�

��1�����B��ˮƽ��AE�ĸ߶�BH��
��2��������CD�ĸ߶ȣ�
��������ĸ߶Ⱥ��Բ��ƣ������ȷ��0.1�����ο����ݣ�![]() 1.414��
1.414��![]() 1.732��
1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��ԲO��ֱ������CD��AB������ΪH����ACƽ�е�ԲO��һ�����߽�CD���ӳ����ڵ�M����AB���ӳ����ڵ�E���е�ΪF������AF��CD�ڵ�N��
��1����֤��CA=CN��
��2������DF����cos��DFA=![]() ��AN=
��AN=![]() ����ԲO��ֱ���ij��ȣ�
����ԲO��ֱ���ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1��ax2��bx��c(a��0)ͼ���һ���֣������ߵĶ�������A(1��3)����x���һ������B(4��0)��ֱ��y2��mx��n(m��0)�������߽���A��B���㣬���н��ۣ���2a��b��0����abc>0���۷���ax2��bx��c��3��������ȵ�ʵ����������������x�����һ��������(��1��0)������1<x<4ʱ����y2<y1��������ȷ���ǣ���
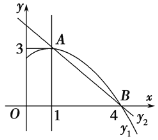
A.�٢ܢ�B.�٢ۢܢ�C.�٢ۢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijУ��չ�����������й���Ϊ�������Ӱ������Ҫ�����ѧ��ÿ�˽�һ����Ʒ���ֽ�
������ѡ��50��������Ʒ�ijɼ�����λ������ͳ�����£�
�ȼ� | �ɼ�����m��ʾ�� | Ƶ�� | Ƶ�� |
A | 90�� m ��100 | x | 0.08 |
B | 80�� m ��90 | 34 | y |
C | m ��80 | 12 | 0.24 |
�ϼ� |
| 50 | 1 |
������ϱ��ṩ����Ϣ������������⣺
��1������![]() ��ֵΪ_____________��
��ֵΪ_____________��![]() ��ֵΪ______________����ֱ����д�����
��ֵΪ______________����ֱ����д�����
��2�������β�����Ʒ���A�ȼ���ѧ��������A1��A2��A3������ʾ���ָ�У�����ӱ��β�����Ʒ���A�ȼ���ѧ���У������ȡ����ѧ��̸̸���ǵIJ�����ᣬ��ǡ�ó鵽ѧ��A1��A2�ĸ���Ϊ____________����ֱ����д�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
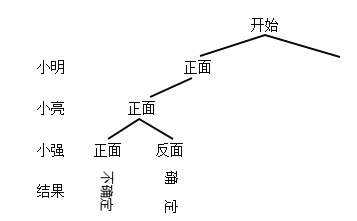
����Ŀ��С����С����Сǿ�����������壬����Լ��������Ӳ��������Ϸ��ʽ��ȷ���ĸ��������壬�������£��������и�����һö�ʵؾ��ȵ�Ӳ�ң�����ͬʱ������Ӳ�����䵽ˮƽ����Ϊһ���غϣ���غ���öӲ���У�ǡ����ö�������ϻ��߷������ϵ����������壻����öӲ�Ҿ�Ϊ�������ϻ������ϣ�����ȷ���������������壮
��1��������������ʾ��Ϸһ���غ����п��ܳ��ֵĽ������״ͼ��
��2�����һ���غ���ȷ����������ĸ��ʣ�
�⣺��1����״ͼΪ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��չ���̻����硢ֲ�����������Ϊ�˽�ȫУֲ��������Ը�У�ס��ҡ�����
���ĸ��༶ֲ����������˵��飬���ռ����������������Ƴ�ͼ1��ͼ2�����в�������ͳ��ͼ�������ͼ�е���Ϣ������������⣺
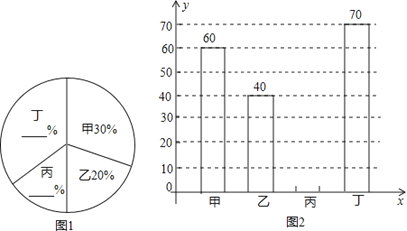
��1�����ĸ��ֲ���� ���ã�
��2�������ڴ���ϲ�ȫ����ͳ��ͼ��
��3����ͼ1���������༶����Ӧ������Բ�ĽǵĶ�����
��4�����ĸ��༶ֲ����ƽ���ɻ�����95%��ȫУ��ֲ��2000�ã��������ȫУ��ֲ�����гɻ�����ж��ٿã�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com