
����Ŀ���ס���������ͬһ����·��![]() �س�����1200
�س�����1200![]() ���
���![]() �����ͽ������ʣ�����;����Ϣ��3Сʱ����Ϣǰ����ٶȲ�ͬ���������ͬʱ����
�����ͽ������ʣ�����;����Ϣ��3Сʱ����Ϣǰ����ٶȲ�ͬ���������ͬʱ����![]() �أ���ͼ�ס���������
�أ���ͼ�ס���������![]() �صľ���
�صľ���![]() ��ǧ�ף����ҳ���ʻʱ��
��ǧ�ף����ҳ���ʻʱ��![]() ��Сʱ��֮��ĺ���ͼ��
��Сʱ��֮��ĺ���ͼ��
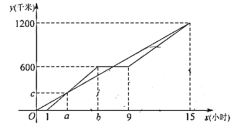
��1���׳���Ϣǰ����ʻ�ٶ�Ϊ ǧ��/ʱ���ҳ����ٶ�Ϊ ǧ��/ʱ��
��2����9��![]() ��15����׳�����ʻ·��
��15����׳�����ʻ·��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3��ֱ��д���׳����ʱ��������;��������
���𰸡���1��120��80����2��![]() ����3��2Сʱ��6.5Сʱ
����3��2Сʱ��6.5Сʱ
��������
��1�����ݼ���;����Ϣ��3Сʱ����Ϻ���ͼ������b��ֵ��������·�̡�ʱ��=�ٶȣ������ý����
��2���ô���ϵ�������н���ɣ�
��3����׳���![]() Сʱ������;��������������������ڼ���;��Ϣǰ����������;��Ϣʱ�������ֱ��г�һԪһ�η��̽��
Сʱ������;��������������������ڼ���;��Ϣǰ����������;��Ϣʱ�������ֱ��г�һԪһ�η��̽��
����ͼ�οɵã�
�ҳ��ӳ������յ㹲��ʱ15Сʱ·��1200ǧ�ף������ҳ����ٶ�=1200��15=80ǧ��/ʱ��
�׳�����ʱ14Сʱ����Ϣ3Сʱ����Ϣ����ʻ6Сʱ��������Ϣǰ��ʻ5Сʱ����Ϣǰ��ʻ·��600ǧ�ף��׳���Ϣǰ����ʻ�ٶ�=600��5=120ǧ��/ʱ��
�ʴ�Ϊ��120��80��
��2���赱![]() ʱ���׳���ʻ·��
ʱ���׳���ʻ·��![]() ��
��![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��
��
�ѵ�![]() ��
��![]() ����ɵã�
����ɵã�
![]() ����ã�
����ã�![]() ��
��
��![]() ʱ���׳���ʻ·��
ʱ���׳���ʻ·��![]() ��
��![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ��
��
��3����׳���xСʱ������;����������������ã�
���ڼ�;����Ϣǰ��������120x-80x=80��1��
��ã�x=2��
���ڼ�;����Ϣʱ��������80��x+1��=600��
��ã�x=6.5��
���ϣ��׳���2Сʱ��6.5Сʱ������;����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������̽����
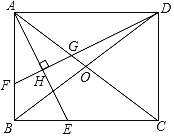
��ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AEƽ�֡�BAC����BC�ڵ�E����DF��AE�ڵ�H���ֱ�AB��AC�ڵ�F��G��
��1���жϡ�AFG����״��˵�����ɣ�
��2����֤��BF=2OG��
��Ǩ��Ӧ�ã�
��3���ǡ�DGO�����ΪS1����DBF�����ΪS2����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
����չ���죩
��4����DF������AB�ڵ�F��������̽�����е������������䣬����EF������BEF�����Ϊ����ABCD�����![]() ʱ����ֱ��д��tan��BAE��ֵ��
ʱ����ֱ��д��tan��BAE��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
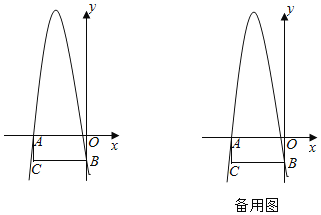
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����AOBC�ı�AO��x��ĸ������ϣ���OB��y��ĸ������ϣ���AO��12��OB��9��������y����x2+bx+c������A�͵�B��
��1���������ߵı���ʽ��
��2���ڵڶ���������������һ��M������AM��BM��AB������ABM������ʱ�����M�����ꣻ
��3����D���߶�AO�ϵĶ��㣬��E���߶�BO�ϵĶ��㣬��F������AC�ϵĶ��㣬����EF��DF��DE��BD����EF���߶�BD�Ĵ�ֱƽ���ߣ���CF��1ʱ��
��ֱ��д����D�������� ����
������DEF�����Ϊ30����������y����x2+bx+c����ƽ��ͬʱ����D�͵�Eʱ����ֱ��д����ʱ�������ߵı���ʽ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
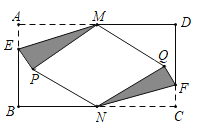
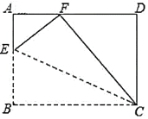
����Ŀ����ͼ�� �ھ���ֽƬ![]() �У�
�� ![]() �� ��
�� ��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬 ��
���е㣬 ��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ� ��
�ϣ� ��![]() .��
.��![]() ��
��![]() �۵��� ��
�۵��� ��![]() �Ķ�Ӧ��Ϊ��
�Ķ�Ӧ��Ϊ��![]() ����
����![]() ��
��![]() �۵��� ��
�۵��� ��![]() �Ķ�Ӧ��Ϊ��
�Ķ�Ӧ��Ϊ��![]() �����ı���
�����ı���![]() Ϊ����ʱ�� ��
Ϊ����ʱ�� ��![]() _______��
_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��3��
��3��![]() ��5��
��5��![]() ��
��![]() ��һ�㣬����
��һ�㣬����![]() ����
����![]() ��
��![]() ���ۣ�ʹ��
���ۣ�ʹ��![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ���ڱ�
���ڱ�![]() �ϣ�����
�ϣ�����![]() �����Ϊ__________��
�����Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
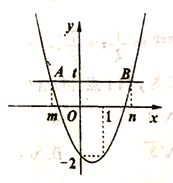
����Ŀ����ͼΪ���κ���![]() ͼ��ֱ��
ͼ��ֱ��![]() �������߽���
�������߽���![]() ����,
����,![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ���ݺ���ͼ����Ϣ�����н���:
���ݺ���ͼ����Ϣ�����н���:
��![]() ;
;
��������![]() ������ֵ����
������ֵ����![]() ,��
,��![]() ;
;
��![]() ;
;
��![]() ;
;
�ݵ�![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ���,���߶�
���,���߶�![]() �䳤
�䳤
���У���ȷ�Ľ�����__________(д��������ȷ���۵ķ���)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
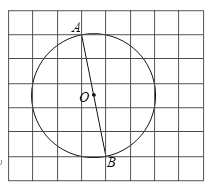
����Ŀ����ͼ����ÿ��С�����εı߳�Ϊ![]() �������У���
����������![]() ����
����![]() �����ڸ���ϣ�
�����ڸ���ϣ�![]() Ϊ��
Ϊ��![]() ��ֱ����
��ֱ����
��1��![]() �ij�����__________��
�ij�����__________��
��2��������ͼ��ʾ�������У����̶���ֱ�ߣ�����һ����![]() Ϊб�ߡ����Ϊ
Ϊб�ߡ����Ϊ![]() ��
��![]() ������Ҫ˵����
������Ҫ˵����![]() ��λ��������ҵ��ģ���Ҫ��֤����__________��
��λ��������ҵ��ģ���Ҫ��֤����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��ͼ��
��ͼ��![]() б��
б��![]() ���е�
���е�![]() ����ֱ�DZ�
����ֱ�DZ�![]() �ཻ��
�ཻ��![]() ������
������![]() ����
����![]() ����
����![]() ���ܳ�Ϊ�� ��
���ܳ�Ϊ�� ��
A.12B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
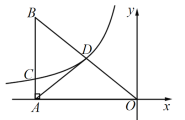
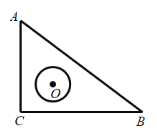
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() �������ƶ�����
�������ƶ�����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��Բ��O��
��Բ��O��![]() �����ܵ������������Ϊ
�����ܵ������������Ϊ![]() ��
��![]() ���ܳ�Ϊ_______________________��
���ܳ�Ϊ_______________________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com