
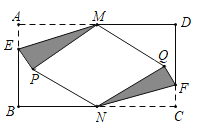
【题目】如图, 在矩形纸片![]() 中,
中, ![]() , 点
, 点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点, 点
的中点, 点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上, 且
上, 且![]() .将
.将![]() 沿
沿![]() 折叠, 点
折叠, 点![]() 的对应点为点
的对应点为点![]() ,将
,将![]() 沿
沿![]() 折叠, 点
折叠, 点![]() 的对应点为点
的对应点为点![]() ,当四边形
,当四边形![]() 为菱形时, 则
为菱形时, 则![]() _______.
_______.
【答案】![]()
【解析】
连接MN,PQ交于点O,延长PQ交CD于H,延长QP交AB于G.解直角三角形求出AG,EG即可解决问题.
如图,连接MN,PQ交于点O,延长PQ交CD于H,延长QP交AB于G.

∵四边形PNQM是菱形,
∴MN⊥PQ,
∵点M、N分别是AD、BC的中点,
∴AM=BN,
又∵矩形ABCD中,AM∥BN,∠A=90°,
∴四边形AMNB是矩形,
∴∠AMN=90°
∴PQ∥AD∥BC,
∴AG=DK=OM=![]() AB=
AB=![]() AD=1,
AD=1,
∵PM=AM=2,
∴sin∠MPO=![]() ,
,
∴∠MPO=30°,
∵∠EPM=90°,
∴∠EPG=90°-30°=60°
∴OP=![]() OM=
OM=![]() ,
,
∵OG=2,
∴EG=PGtan60°=2![]() -3,
-3,
∴GP=2-![]() ,
,
∴AE=AG-EG=1-(2![]() -3)=4-2
-3)=4-2![]() .
.
故答案为:4-2![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
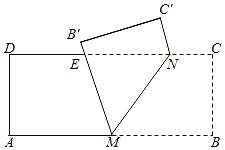
【题目】如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N分别在边AB,CD上,CN=1cm.现将四边形BCNM沿MN折叠,使点B,C分别落在点B',C'上.当点B'恰好落在边CD上时,线段BM的长为_____cm;在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴正半轴上,以
轴正半轴上,以![]() 为一边作等腰直角
为一边作等腰直角![]() ,使得点
,使得点![]() 在第一象限.
在第一象限.

(1)求出所有符合题意的点![]() 的坐标;
的坐标;
(2)在![]() 内部存在一点
内部存在一点![]() ,使得
,使得![]() 之和最小,请求出这个和的最小值.
之和最小,请求出这个和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+6的图像开口向下,与x轴交于点A(-6,0)和点B(2,0),与y轴交于点C,点P是该函数图像上的一个动点(不与点C重合)

(1) 求二次函数的关系式;
(2)如图1当点P是该函数图像上一个动点且在线段![]() 的上方,若△PCA的面积为12,求点P的坐标;
的上方,若△PCA的面积为12,求点P的坐标;
(3)如图2,该函数图像的顶点为D,在该函数图像上是否存在点E,使得∠EAB=2∠DAC,若存在请直接写出点E的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方法回顾)
课本研究三角形中位线性质的方法
已知:如图①, 已知![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 两边中点.
两边中点.
求证:![]() ,
,![]()
证明:延长![]() 至点
至点![]() ,使
,使![]() , 连按
, 连按![]() .可证:
.可证:![]() ( )
( )
由此得到四边形![]() 为平行四边形, 进而得到求证结论
为平行四边形, 进而得到求证结论
(1)请根据以上证明过程,解答下列两个问题:
①在图①中作出证明中所描述的辅助线(请用![]() 铅笔作辅助线);
铅笔作辅助线);
②在证明的括号中填写理由(请在![]() ,
,![]() ,
,![]() ,
,![]() 中选择) .
中选择) .
(问题拓展)
(2)如图②,在等边![]() 中, 点
中, 点![]() 是射线
是射线![]() 上一动点(点
上一动点(点![]() 在点
在点![]() 的右侧),把线段
的右侧),把线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() 、
、![]() .
.
①请你判断线段![]() 与
与![]() 的数量关系,并给出证明;
的数量关系,并给出证明;
②若![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
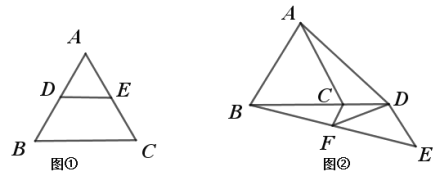
查看答案和解析>>
科目:初中数学 来源: 题型:
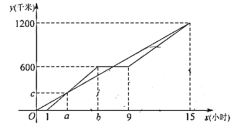
【题目】甲、乙两车沿同一条道路从![]() 地出发向1200
地出发向1200![]() 外的
外的![]() 地输送紧急物资,甲在途中休息了3小时,休息前后的速度不同,最后两车同时到达
地输送紧急物资,甲在途中休息了3小时,休息前后的速度不同,最后两车同时到达![]() 地,如图甲、乙两车到
地,如图甲、乙两车到![]() 地的距离
地的距离![]() (千米)与乙车行驶时间
(千米)与乙车行驶时间![]() (小时)之间的函数图象.
(小时)之间的函数图象.
(1)甲车休息前的行驶速度为 千米/时,乙车的速度为 千米/时;
(2)当9≤![]() ≤15,求甲车的行驶路程
≤15,求甲车的行驶路程![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)直接写出甲出发多长时间与乙在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数,
为常数,![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点.设该抛物线的顶点为
点.设该抛物线的顶点为![]() ,其对称轴与
,其对称轴与![]() 轴的交点为
轴的交点为![]() .
.
(1)求该抛物线的解析式;
(2)![]() 为线段
为线段![]() (含端点
(含端点![]() )上一点,
)上一点,![]() 为
为![]() 轴上一点,且
轴上一点,且![]() .
.
①求![]() 的取值范围;
的取值范围;
②当![]() 取最大值时,将线段
取最大值时,将线段![]() 向上平移
向上平移![]() 个单位长度,使得线段
个单位长度,使得线段![]() 与抛物线有两个交点,求
与抛物线有两个交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
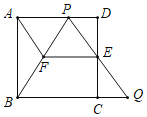
【题目】如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:![]() ;
;
(2)过点E作![]() 交PB于点F,连结AF,当
交PB于点F,连结AF,当![]() 时,①求证:四边形AFEP是平行四边形;
时,①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com