
【题目】抛物线![]() (
(![]() 为常数,
为常数,![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点.设该抛物线的顶点为
点.设该抛物线的顶点为![]() ,其对称轴与
,其对称轴与![]() 轴的交点为
轴的交点为![]() .
.
(1)求该抛物线的解析式;
(2)![]() 为线段
为线段![]() (含端点
(含端点![]() )上一点,
)上一点,![]() 为
为![]() 轴上一点,且
轴上一点,且![]() .
.
①求![]() 的取值范围;
的取值范围;
②当![]() 取最大值时,将线段
取最大值时,将线段![]() 向上平移
向上平移![]() 个单位长度,使得线段
个单位长度,使得线段![]() 与抛物线有两个交点,求
与抛物线有两个交点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)利用待定系数法将A和B的坐标代入求解即可;
(2)①抛物线的对称轴为:x=2,顶点M(2,4),在Rt△PCQ中,由勾股定理得:PC2+PQ2=CQ2,把三角形三边长用点P,Q的坐标表达出来,整理得:![]() ,利用0≤m≤4,求出n的取值范围;
,利用0≤m≤4,求出n的取值范围;
②设线段CQ向上平移t个单位长度后的解析式为:![]() 联立抛物线方程,可求出x2-7x+4t=0,由△=49-16t=0,得
联立抛物线方程,可求出x2-7x+4t=0,由△=49-16t=0,得![]() ,可得当线段CQ与抛物线有两个交点时,
,可得当线段CQ与抛物线有两个交点时,![]() .
.
解:(1)∵ 点![]() ,
,![]() 在抛物线上,
在抛物线上,
∴ ![]()
解得![]() ,
,![]() .
.
∴ 该抛物线的解析式为![]() ;
;
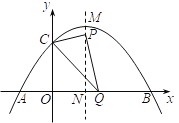
(2)① 由![]() ,得
,得![]() (2,4),
(2,4),
设![]() 点坐标为(2,m),其中
点坐标为(2,m),其中![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴在△PCQ中,![]() ,
,
即![]() ,
,
整理得![]() ,0≤m≤4,
,0≤m≤4,
∴当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() ;
;
当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() ;
;
②由①知,当![]() 取最大值4时,
取最大值4时,![]() .此时
.此时![]() ,
,
∵点![]() ,
,
∴线段![]() 的解析式为
的解析式为![]() ,
,
设![]() 向上平移
向上平移![]() 个单位长度后的解析式为
个单位长度后的解析式为![]() .
.
如图,当线段![]() 向上平移,使点
向上平移,使点![]() 恰好在抛物线上时,线段
恰好在抛物线上时,线段![]() 与抛物线有两个交点,此时点
与抛物线有两个交点,此时点![]() 的坐标
的坐标![]() .
.
将![]() 代入
代入![]() ,得
,得![]() .
.
当线段![]() 继续向上平移,线段
继续向上平移,线段![]() 与抛物线只有一个交点时,
与抛物线只有一个交点时,
由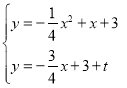 ,
,
得![]() .化简,得
.化简,得![]() .
.
由![]() ,解得
,解得![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
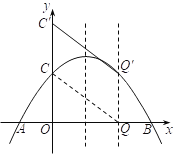
【题目】如图,在由边长为1个单位长度的小正方形组成的8×9的网格中,已知△ABC的顶点均为网格线的交点.
(1)在给定的网格中,画出△ABC关于直线AB对称的△ABC1.
(2)将△ABC1绕着点O旋转后能与△ABC重合,请在网格中画出点O的位置.
(3)在给定的网格中,画出以点C为位似中心,将△ABC放大为原来的2倍后得到的△A2B2C.
查看答案和解析>>
科目:初中数学 来源: 题型:
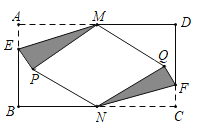
【题目】如图, 在矩形纸片![]() 中,
中, ![]() , 点
, 点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点, 点
的中点, 点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上, 且
上, 且![]() .将
.将![]() 沿
沿![]() 折叠, 点
折叠, 点![]() 的对应点为点
的对应点为点![]() ,将
,将![]() 沿
沿![]() 折叠, 点
折叠, 点![]() 的对应点为点
的对应点为点![]() ,当四边形
,当四边形![]() 为菱形时, 则
为菱形时, 则![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
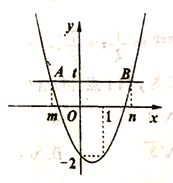
【题目】如图为二次函数![]() 图象,直线
图象,直线![]() 与抛物线交于
与抛物线交于![]() 两点,
两点,![]() 两点横坐标分别为
两点横坐标分别为![]() 根据函数图象信息有下列结论:
根据函数图象信息有下列结论:
①![]() ;
;
②若对于![]() 的任意值都有
的任意值都有![]() ,则
,则![]() ;
;
③![]() ;
;
④![]() ;
;
⑤当![]() 为定值时若
为定值时若![]() 变大,则线段
变大,则线段![]() 变长
变长
其中,正确的结论有__________(写出所有正确结论的番号)
查看答案和解析>>
科目:初中数学 来源: 题型:
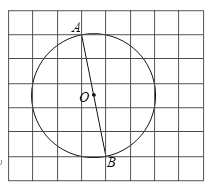
【题目】如图,在每个小正方形的边长为![]() 的网格中,点
的网格中,点![]() ,点
,点![]() 均落在格点上,
均落在格点上,![]() 为⊙
为⊙![]() 的直径.
的直径.
(1)![]() 的长等于__________;
的长等于__________;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个以![]() 为斜边、面积为
为斜边、面积为![]() 的
的![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]()
![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() .
.
(1)若![]() ,求
,求![]() ,
,![]() 满足的关系式;
满足的关系式;
(2)直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,抛物线的对称轴为直线
两点,抛物线的对称轴为直线![]() ,且
,且![]() .
.
①求抛物线的解析式(各项系数用含![]() 的式子表示);
的式子表示);
②求线段![]() 长度的取值范围.
长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
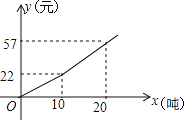
【题目】为鼓励市民节约用水,某市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系
(1)小红家五月份用水8吨,应交水费_____元;
(2)按上述分段收费标准,小红家三、四月份分别交水费36元和19.8元,问四月份比三月份节约用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
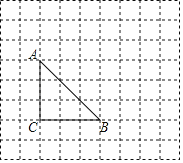
【题目】如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com