
【题目】如图,四边形ABCD是矩形,点A在第四象限y1=﹣![]() 的图象上,点B在第一象限y2=
的图象上,点B在第一象限y2=![]() 的图象上,AB交x轴于点E,点C与点D在y轴上,AD=
的图象上,AB交x轴于点E,点C与点D在y轴上,AD=![]() ,S矩形OCBE=
,S矩形OCBE=![]() S矩形ODAE.
S矩形ODAE.
(1)求点B的坐标.
(2)若点P在x轴上,S△BPE=3,求直线BP的解析式.

【答案】(1)B(![]() ,2);(2)直线BP的解析式是y=
,2);(2)直线BP的解析式是y=![]() x+1或y=﹣
x+1或y=﹣![]() x+3.
x+3.
【解析】
(1)根据反比例函数系数k的几何意义求得k=3,得出![]() ,由题意可知B的横坐标为
,由题意可知B的横坐标为![]() ,代入即可求得B的坐标;
,代入即可求得B的坐标;
(2)设P(a,0),根据三角形面积求得P的坐标,然后根据待定系数法即可求得直线BP的解析式.
(1)∵S矩形OCBE=![]() S矩形ODAE,点B在第一象限y2=
S矩形ODAE,点B在第一象限y2=![]() 的图象上,
的图象上,
∵点A在第四象限y1=﹣![]() 的图象上,
的图象上,
∴S矩形ODEA=2
∴S矩形OCBE=![]() ×2=3,
×2=3,
∴k=3,
∴y2=![]() ,
,
∵OE=AD=![]() ,
,
∴B的横坐标为![]() ,
,
代入y2=![]() 得,y=
得,y=![]() =2,
=2,
∴B(![]() ,2);
,2);
(2)设P(a,0),
∵S△BPE=![]() PEBE=
PEBE=![]() ,
,
解得a=﹣![]() 或
或![]() ,
,
∴点P(﹣![]() ,0)或(
,0)或(![]() ,0),
,0),
设直线BP的解析式为y=mx+n(m≠0),
①若直线过(![]() ,2),(﹣
,2),(﹣![]() ,0),
,0),
则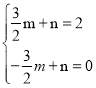 ,解得
,解得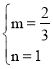 ,
,
∴直线BP的解析式为y=![]() x+1;
x+1;
②若直线过(![]() ,2),(
,2),(![]() ,0),
,0),
则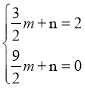 ,解得
,解得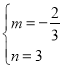 ,
,
∴直线BP的解析式为y=﹣![]() x+3;
x+3;
综上,直线BP的解析式是y=![]() x+1或y=﹣
x+1或y=﹣![]() x+3.
x+3.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,为了绿化小区,某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH.
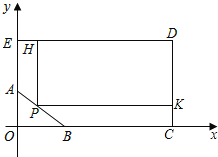
已知:![]() ,DE=100米,EA=60米,BC=70米,CD=80米.以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为O.
,DE=100米,EA=60米,BC=70米,CD=80米.以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为O.
(1)求直线AB的解析式.
(2)若设点P的横坐标为x,矩形PKDH的面积为S,求S关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过点A(3,4)的抛物线y=ax2+bx+4与x轴交于点B(﹣1,0),与y轴交于点C,过点A作AD⊥x轴于点D.

(1)求抛物线的解析式.
(2)如图1,点P是直线AB上方抛物线上的一个动点,连接PD交AB于点Q,连接AP,当S△AQD=2S△APQ时,求点P的坐标.
(3)如图2,G是线段OC上一个动点,连接DG,过点G作GM⊥DG交AC于点M,过点M作射线MN,使∠NMG=60°,交射线GD于点N;过点G作GH⊥MN,垂足为点H,连接BH.请直接写出线段BH的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以点A为圆心、AB的长为半径画弧交AD于点F,再分别以点B,F为圆心、大于![]() BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )
BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )

A. BE=EFB. EF∥CDC. AE平分∠BEFD. AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
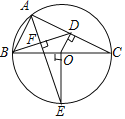
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D,连接BD,半径OE⊥BC,连接EA,EA⊥BD于点F.若OD=2,则BC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“足球进校园”的号召,我县教体局在今年 11 月份组织了“县长杯”校园足球比赛.在某场比赛中,一个球被从地面向上踢出,它距地面的高度 h(m)可用公式 h=﹣5t2+v0t 表示,其中 t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果足球的最大高度到 20m,那么足球被踢出时的速度应达到________m/s.
查看答案和解析>>
科目:初中数学 来源: 题型:
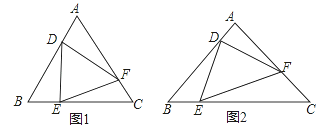
【题目】定义:在△ABC中,点D,E,F分别是边AB,BC,CA上的动点,若△DEF∽△ABC(点D、E、F的对应点分别为点A、B、C),则称△DEF是△ABC的子三角形,如图.
(1)已知:如图1,△ABC是等边三角形,点D,E,F分别是边AB,BC,CA上动点,且AD=BE=CF.
求证:△DEF是△ABC的子三角形.
(2)已知:如图2,△DEF是△ABC的子三角形,且AB=AC,∠A=90°,若BE=![]() ,求CF和AD的长.
,求CF和AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,AB=5,若以C为圆心,r为半径作圆,那么:

(1)当直线AB与⊙C相切时,求r的取值范围;
(2)当直线AB与⊙C相离时,求r的取值范围;
(3)当直线AB与⊙C相交时,求r的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com