
【题目】如图,Rt△ABC中,∠C=90°,AC=3,AB=5,若以C为圆心,r为半径作圆,那么:

(1)当直线AB与⊙C相切时,求r的取值范围;
(2)当直线AB与⊙C相离时,求r的取值范围;
(3)当直线AB与⊙C相交时,求r的取值范围.
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点A在第四象限y1=﹣![]() 的图象上,点B在第一象限y2=
的图象上,点B在第一象限y2=![]() 的图象上,AB交x轴于点E,点C与点D在y轴上,AD=
的图象上,AB交x轴于点E,点C与点D在y轴上,AD=![]() ,S矩形OCBE=
,S矩形OCBE=![]() S矩形ODAE.
S矩形ODAE.
(1)求点B的坐标.
(2)若点P在x轴上,S△BPE=3,求直线BP的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
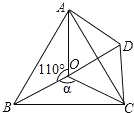
(1)试说明△COD是等边三角形;
(2)当a=150°时,OB=3,OC=4,试求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=2x2-8x+6.
(1)利用配方法写出这个函数图象的开口方向、对称轴、顶点坐标.
(2)在下面的平面直角坐标系中画图此函数图象.
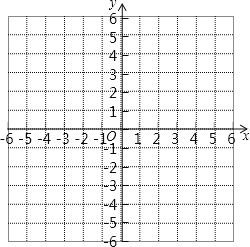
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①频率是反映事件发生的频繁程度,概率反映事件发生的可能性大小;②做n次随机试验,事件A发生m次,则事件A发生的概率一定等于![]() ;③频率是不能脱离具体的n次试验的实验值,而概率是具有确定性的不依赖于试验次数的理论值;④频率是概率的近似值,概率是频率的稳定值.其中正确的是______(填序号).
;③频率是不能脱离具体的n次试验的实验值,而概率是具有确定性的不依赖于试验次数的理论值;④频率是概率的近似值,概率是频率的稳定值.其中正确的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,对角线AC,BD相交于点O,AB=2厘米,∠BAD=60°。P,Q两点同时从点O出发,以1厘米/秒的速度在菱形的对角线及边上运动。设运动的时间为x秒,P,Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,则P、Q的运动路线可能为( )
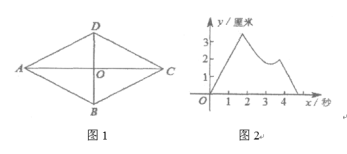
A. 点P:O→A→D→C,点Q:O→C→D→O
B. 点P:O→A→B→C,点Q:O→C→D→O
C. 点P:O→A→D→O,点Q:O→C→D→O
D. 点P:O→A→D→O,点Q:O→C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图①,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
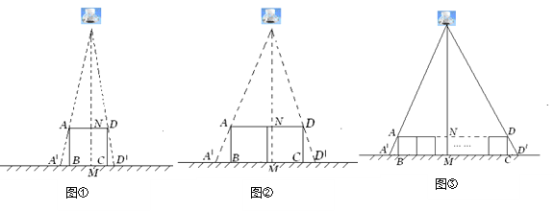 (2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图③摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
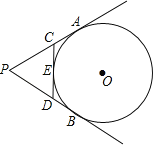
【题目】如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com