
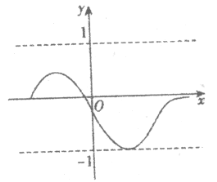
ЎѕМвДїЎїИзНј1Ј¬ЛД±ЯРОABCDКЗБвРОЈ¬¶ФЅЗПЯACЈ¬BDПаЅ»УЪµгOЈ¬AB=2АеГЧЈ¬ЎПBAD=60ЎгЎЈPЈ¬QБЅµгН¬К±ґУµгOіц·ўЈ¬ТФ1АеГЧ/ГлµДЛЩ¶ИФЪБвРОµД¶ФЅЗПЯј°±ЯЙПФЛ¶ЇЎЈЙиФЛ¶ЇµДК±јдОЄxГлЈ¬PЈ¬QјдµДѕаАлОЄyАеГЧЈ¬yУлxµДєЇКэ№ШПµµДНјПуґуЦВИзНј2ЛщКѕЈ¬ФтPЎўQµДФЛ¶ЇВ·ПЯїЙДЬОЄЈЁ Ј©
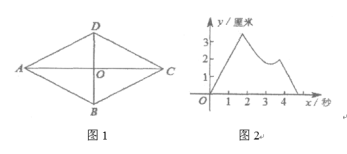
A. µгPЈєOЎъAЎъDЎъCЈ¬µгQЈєOЎъCЎъDЎъO
B. µгPЈєOЎъAЎъBЎъCЈ¬µгQЈєOЎъCЎъDЎъO
C. µгPЈєOЎъAЎъDЎъOЈ¬µгQЈєOЎъCЎъDЎъO
D. µгPЈєOЎъAЎъDЎъOЈ¬µгQЈєOЎъCЎъBЎъO
Ўѕґр°ёЎїD
ЎѕЅвОцЎї
ПИёщѕЭНј1ЦРІ»Н¬В·ПЯµДО»ЦГЈ¬ЕР¶ПPЈ¬QјдµДѕаАлµД±д»»ЗйїцЈ¬ФЩЅбєПНј2ЦРєЇКэНјПуµД±д»»ЗчКЖЅшРРЕР¶П·ЦОцЈ®
ЅвЈєЎЯБвРОABCDЦРЈ¬AB=2Ј¬ЎПBAD=60Ўг
ЎаAO=CO=![]() Ј¬DO=BO=1
Ј¬DO=BO=1
AЎўИфµгPЈєO-A-D-CЈ¬µгQЈєO-C-D-OЈ¬Фтµ±x=2+![]() К±Ј¬y=0Ј¬УлНј2І»·ыЈ¬№КAґнОуЈ»
К±Ј¬y=0Ј¬УлНј2І»·ыЈ¬№КAґнОуЈ»
BЎўµ±µгPУлµгQФЛ¶ЇНкК±Ј¬µгPФЪµгCЙПЈ¬µгQФЪµгOЙПЈ¬ЛщТФy=![]() Ј¬УлНј2І»·ыЈ¬№КBґнОуЈ»
Ј¬УлНј2І»·ыЈ¬№КBґнОуЈ»
CЎўИфµгPЈєO-A-D-OЈ¬µгQЈєO-C-D-OЈ¬Фтµ±x=2+![]() К±Ј¬y=0Ј¬УлНј2І»·ыЈ¬№КCґнОуЈ»
К±Ј¬y=0Ј¬УлНј2І»·ыЈ¬№КCґнОуЈ»
DЎўИфµгPЈєO-A-D-OЈ¬µгQЈєO-C-B-OЈ¬Фтµ±x=![]() К±Ј¬yУРЧоґуЦµЈ¬µ±x=
К±Ј¬yУРЧоґуЦµЈ¬µ±x=![]() +
+![]() К±Ј¬y=
К±Ј¬y=![]() Ј¬µ±x=3+
Ј¬µ±x=3+![]() К±Ј¬y=0Ј¬УлНј2Па·ыЈ¬№КDХэИ·Ј®
К±Ј¬y=0Ј¬УлНј2Па·ыЈ¬№КDХэИ·Ј®
№КСЎЈєDЈ®


 МмМмПтЙПТ»±ѕєГѕнПµБРґр°ё
МмМмПтЙПТ»±ѕєГѕнПµБРґр°ё РЎС§Йъ10·ЦЦУУ¦УГМвПµБРґр°ё
РЎС§Йъ10·ЦЦУУ¦УГМвПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄПмУ¦Ў°ЧгЗтЅшРЈФ°Ў±µДєЕХЩЈ¬ОТПШЅММеѕЦФЪЅсДк 11 ФВ·ЭЧйЦЇБЛЎ°ПШі¤±Ў±РЈФ°ЧгЗт±ИИьЈ®ФЪДііЎ±ИИьЦРЈ¬Т»ёцЗт±»ґУµШГжПтЙПМЯіцЈ¬ЛьѕаµШГжµДёЯ¶И h(m)їЙУГ№«КЅ hЈЅ©Ѓ5t2+v0t ±нКѕЈ¬ЖдЦР t(s)±нКѕЧгЗт±»МЯіцєуѕ№эµДК±јдЈ¬v0(m/s)КЗЧгЗт±»МЯіцК±µДЛЩ¶ИЈ¬Из№ыЧгЗтµДЧоґуёЯ¶ИµЅ 20mЈ¬ДЗГґЧгЗт±»МЯіцК±µДЛЩ¶ИУ¦ґпµЅ________m/sЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄі¤·ЅРОУІЦЅ°еABCDµДі¤BCОЄ40cmЈ¬їнCDОЄ30cmЈ¬°ґИзНјЛщКѕјфµф2ёцРЎХэ·ЅРОєН2ёцРЎі¤·ЅРОЈЁјґНјЦРТхУ°Ії·ЦЈ©Ј¬Ѕ«КЈУаІї·ЦХЫіЙТ»ёцУРёЗµДі¤·ЅМеєРЧУЈ¬
ЙијфµфµДРЎХэ·ЅРО±Яі¤ОЄxcmЈ®ЈЁЦЅ°еµДєс¶ИєцВФІ»јЖЈ©
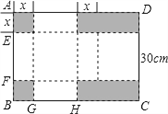
ЈЁ1Ј©МоїХЈєEF= Ј®cmЈ¬GH= Ј®cmЈ»ЈЁУГє¬xµДґъКэКЅ±нКѕЈ©
ЈЁ2Ј©ИфХЫіЙµДі¤·ЅМеєРЧУµД±нГж»эОЄ950cm2Ј¬ЗуёГі¤·ЅМеєРЧУµДМе»э
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬RtЎчABCЦРЈ¬ЎПC=90ЎгЈ¬AC=3Ј¬AB=5Ј¬ИфТФCОЄФІРДЈ¬rОЄ°лѕ¶ЧчФІЈ¬ДЗГґ:

ЈЁ1Ј©µ±Ц±ПЯABУлЎСCПаЗРК±Ј¬ЗуrµДИЎЦµ·¶О§Ј»
ЈЁ2Ј©µ±Ц±ПЯABУлЎСCПаАлК±Ј¬ЗуrµДИЎЦµ·¶О§Ј»
ЈЁ3Ј©µ±Ц±ПЯABУлЎСCПаЅ»К±Ј¬ЗуrµДИЎЦµ·¶О§Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄ№АјЖДіТ»іШМБЦРУгµДЧЬКэДїЈ¬РЎУўЅ«100ОІЧцБЛ±кјЗµДУгН¶ИліШМБЦРЈ¬јёМмєуЈ¬Лж»ъІ¶АМЈ¬ГїґОІ¶АМєуЧцєГјЗВјЈ¬И»єуЅ«Уг·Е»ШЈ¬ИзґЛЅшРР20ґОЈ¬јЗВјКэѕЭИзПВЈє
ЧЬМхКэ | 50 | 45 | 60 | 48 | 10 | 30 | 42 | 38 | 15 | 10 |
±кјЗКэ | 2 | 1 | 3 | 2 | 0 | 1 | 1 | 2 | 0 | 1 |
ЧЬМхКэ | 53 | 36 | 27 | 34 | 43 | 26 | 18 | 22 | 25 | 47 |
±кјЗКэ | 2 | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 2 |
(1)№АјЖіШМБЦРУгµДЧЬКэЈ®ёщѕЭХвЦЦ·Ѕ·Ё№АЛгКЗ·сЧјИ·?
(2)ЗлЙијЖБнТ»ЦЦ±кјЗµД·Ѕ·ЁЈ¬К№µГ№АјЖёьјУѕ«ЧјЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј,ФЪЎчABCЦРЈ¬ЎПACB=90ЎгЈ¬DОЄAB±ЯЙПТ»µгЈ¬Б¬ЅУCDЈ¬EОЄCDµДЦРµгЈ¬Б¬ЅУBEІўСУі¤ЦБµгFЈ¬К№µГEF=EBЈ¬Б¬ЅУDFЅ»ACУЪµгGЈ¬Б¬ЅУCFЈ¬
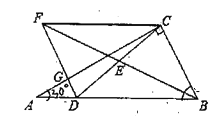
ЈЁ1Ј©ЗуЦ¤ЈєЛД±ЯРОDBCFКЗЖЅРРЛД±ЯРО
ЈЁ2Ј©ИфЎПA=30ЎгЈ¬BC=4Ј¬CF=6Ј¬ЗуCDµДі¤
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї¶ФДіТ»ёцєЇКэёшіцИзПВРВ¶ЁТеЈєИфґжФЪКµКэM>0Ј¬¶ФУЪИОТвµДєЇКэЦµyЈ¬¶јВъЧгЈMЎЬyЎЬMЈ¬ФтіЖХвёцєЇКэКЗґжЅзєЇКэЈ¬ФЪЛщУРВъЧгМхјюµДMЦРЈ¬ЖдЧоРЎЦµіЖОЄХвёцєЇКэµДЅзЦµЎЈАэИзЈ¬ПВНјЦРµДєЇКэКЗґжЅзєЇКэЈ¬ЖдЅзЦµКЗ1ЎЈ
ЈЁ1Ј©·Ц±рЕР¶ПєЇКэ![]() ЈЁx>Ј1Ј©єН
ЈЁx>Ј1Ј©єН![]() ЈЁЈ4<xЎЬ2Ј©КЗІ»КЗґжЅзєЇКэ?ИфКЗґжЅзєЇКэЗуЖдЅзЦµЈ»
ЈЁЈ4<xЎЬ2Ј©КЗІ»КЗґжЅзєЇКэ?ИфКЗґжЅзєЇКэЗуЖдЅзЦµЈ»
ЈЁ2Ј©ИфєЇКэ![]() ЈЁaЎЬxЎЬbЈ¬b>aЈ©µДЅзЦµКЗ2Ј¬ЗТХвёцєЇКэµДЧоґуЦµТІКЗ2Ј¬ЗуbµДИЎЦµ·¶О§Јє
ЈЁaЎЬxЎЬbЈ¬b>aЈ©µДЅзЦµКЗ2Ј¬ЗТХвёцєЇКэµДЧоґуЦµТІКЗ2Ј¬ЗуbµДИЎЦµ·¶О§Јє
ЈЁ3Ј©Ѕ«єЇКэ![]() ЈЁЈ1ЎЬxЎЬmЈ¬mЎЭ0Ј©µДНјПуПтПВЖЅТЖmёцµҐО»Ј¬µГµЅµДєЇКэµДЅзЦµКЗtЈ¬ИфК№
ЈЁЈ1ЎЬxЎЬmЈ¬mЎЭ0Ј©µДНјПуПтПВЖЅТЖmёцµҐО»Ј¬µГµЅµДєЇКэµДЅзЦµКЗtЈ¬ИфК№![]() ЎЬtЎЬ1Ј¬ФтЦ±ЅУРґіцmµДИЎЦµ·¶О§КЗ_____________________________ЎЈ
ЎЬtЎЬ1Ј¬ФтЦ±ЅУРґіцmµДИЎЦµ·¶О§КЗ_____________________________ЎЈ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
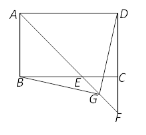
ЎѕМвДїЎїИзНј,ФЪѕШРОABCDЦР,ЎПBADµДЖЅ·ЦПЯЅ»BCУЪµгE,Ѕ»DCµДСУі¤ПЯУЪµгF.
ЈЁ1Ј©ИфAB=2,AD=3,ЗуEFµДі¤Ј»
ЈЁ2Ј©ИфGКЗEFµДЦРµг,Б¬ЅУBGєНDG,ЗуЦ¤ЈєDG=BG.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїБвРОµД¶ФЅЗПЯПаЅ»УЪOЈ¬ТФOОЄФІРДЈ¬ТФµгOµЅБвРОТ»±ЯµДѕаАлОЄ°лѕ¶µДЎСOУлБвРОЖдЛьИэ±ЯµДО»ЦГ№ШПµКЗЈЁ Ј©
A. ПаЅ»B. ПаАлC. ПаЗРD. ОЮ·ЁИ·¶Ё
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com