
【题目】菱形的对角线相交于O,以O为圆心,以点O到菱形一边的距离为半径的⊙O与菱形其它三边的位置关系是( )
A. 相交B. 相离C. 相切D. 无法确定
 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,对角线AC,BD相交于点O,AB=2厘米,∠BAD=60°。P,Q两点同时从点O出发,以1厘米/秒的速度在菱形的对角线及边上运动。设运动的时间为x秒,P,Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,则P、Q的运动路线可能为( )
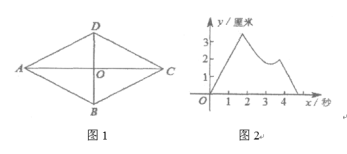
A. 点P:O→A→D→C,点Q:O→C→D→O
B. 点P:O→A→B→C,点Q:O→C→D→O
C. 点P:O→A→D→O,点Q:O→C→D→O
D. 点P:O→A→D→O,点Q:O→C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,P是边AB上一点,AD⊥CP,BE⊥CP,垂足分别为D、E,AC=3,BC=3![]() ,BE=5,DC=
,BE=5,DC=![]() .求证:
.求证:
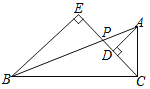
(1)Rt△ACD∽Rt△CBE;
(2)AC⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
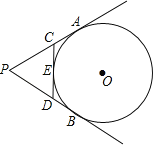
【题目】如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
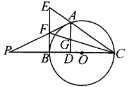
(1)求证:BF=EF;
(2)求证:PA是⊙O的切线;
(3)若FG=BF,且⊙O的半径长为3![]() ,求BD和FG的长度.
,求BD和FG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y1=-![]() x2 和反比例函数y2的图象有一个交点是 A(
x2 和反比例函数y2的图象有一个交点是 A(![]() ,-1).
,-1).
(1)求函数y2的解析式;
(2)在同一直角坐标系中,画出函数y1和y2的图象草图;
(3)借助图象回答:当自变量x在什么范围内取值时,对于x的同一个值,都有y1<y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
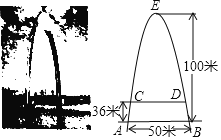
【题目】如图所示是某斜拉索大桥,主索塔呈抛物线,主索塔底部在水面部分的宽度AB=50米,主索塔的最高点E距水面的垂直距离为100米,桥面CD距水面的咨度为36米,则桥的宽度CD_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com