
【题目】已知,如图,在△ABC中,P是边AB上一点,AD⊥CP,BE⊥CP,垂足分别为D、E,AC=3,BC=3![]() ,BE=5,DC=
,BE=5,DC=![]() .求证:
.求证:
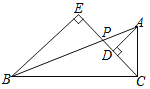
(1)Rt△ACD∽Rt△CBE;
(2)AC⊥BC.
科目:初中数学 来源: 题型:
【题目】已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,
设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)
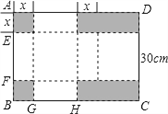
(1)填空:EF= .cm,GH= .cm;(用含x的代数式表示)
(2)若折成的长方体盒子的表面积为950cm2,求该长方体盒子的体积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下新定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是存界函数,在所有满足条件的M中,其最小值称为这个函数的界值。例如,下图中的函数是存界函数,其界值是1。
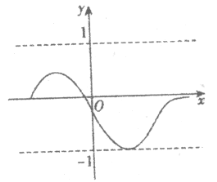
(1)分别判断函数![]() (x>-1)和
(x>-1)和![]() (-4<x≤2)是不是存界函数?若是存界函数求其界值;
(-4<x≤2)是不是存界函数?若是存界函数求其界值;
(2)若函数![]() (a≤x≤b,b>a)的界值是2,且这个函数的最大值也是2,求b的取值范围:
(a≤x≤b,b>a)的界值是2,且这个函数的最大值也是2,求b的取值范围:
(3)将函数![]() (-1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的界值是t,若使
(-1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的界值是t,若使![]() ≤t≤1,则直接写出m的取值范围是_____________________________。
≤t≤1,则直接写出m的取值范围是_____________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
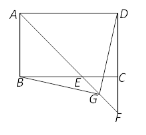
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.
(1)若AB=2,AD=3,求EF的长;
(2)若G是EF的中点,连接BG和DG,求证:DG=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上,则CE:CF=( )
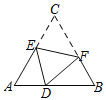
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AB上,以AD为直径的⊙O与边BC相切于点E,与边AC相交于点G,且![]() =
=![]() ,连接GO并延长交⊙O于点F,连接BF
,连接GO并延长交⊙O于点F,连接BF
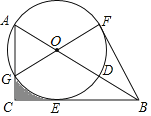
(1)求证:①AO=AG,②BF是⊙O的切线.
(2)若BD=6,求图形中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形的对角线相交于O,以O为圆心,以点O到菱形一边的距离为半径的⊙O与菱形其它三边的位置关系是( )
A. 相交B. 相离C. 相切D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于90%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)符合一次函数关系,如图所示:
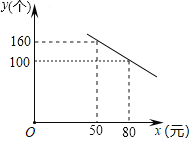
(1)根据图象,直接写出y与x的函数关系式;
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com