
【题目】某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于90%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)符合一次函数关系,如图所示:
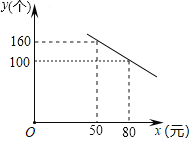
(1)根据图象,直接写出y与x的函数关系式;
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
【答案】(1)y=﹣2x+260;(2)销售单价为80元;(3)销售单价为90元时,每天获得的利润最大,最大利润是3200元.
【解析】
(1)由待定系数法可得函数的解析式;
(2)根据利润等于每件的利润乘以销售量,列方程可解;
(3)设每天获得的利润为w元,由题意得二次函数,写成顶点式,可求得答案.
(1)设y=kx+b(k≠0,b为常数)
将点(50,160),(80,100)代入得
![]()
解得![]()
∴y与x的函数关系式为:y=﹣2x+260
(2)由题意得:(x﹣50)(﹣2x+260)=3000
化简得:x2﹣180x+8000=0
解得:x1=80,x2=100
∵x≤50×(1+90%)=95
∴x2=100>95(不符合题意,舍去)
答:销售单价为80元.
(3)设每天获得的利润为w元,由题意得
w=(x﹣50)(﹣2x+260)
=﹣2x2+360x﹣13000
=﹣2(x﹣90)2+3200
∵a=﹣2<0,抛物线开口向下
∴w有最大值,当x=90时, w最大值=3200
答:销售单价为90元时,每天获得的利润最大,最大利润是3200元.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,P是边AB上一点,AD⊥CP,BE⊥CP,垂足分别为D、E,AC=3,BC=3![]() ,BE=5,DC=
,BE=5,DC=![]() .求证:
.求证:
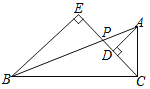
(1)Rt△ACD∽Rt△CBE;
(2)AC⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y1=-![]() x2 和反比例函数y2的图象有一个交点是 A(
x2 和反比例函数y2的图象有一个交点是 A(![]() ,-1).
,-1).
(1)求函数y2的解析式;
(2)在同一直角坐标系中,画出函数y1和y2的图象草图;
(3)借助图象回答:当自变量x在什么范围内取值时,对于x的同一个值,都有y1<y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC的纸片中,∠C=90°,AC=5,AB=13.点D在边BC上,以AD为折痕将△ADB折叠得到△ADB′,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是___.
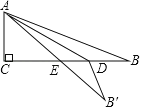
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+2x+c与x轴交于A(﹣1,0)、B(3,0)两点,一次函数y=kx+b的图象l经过抛物线上的点C(m,n)
(1)求抛物线的解析式;
(2)若m=3,直线l与抛物线只有一个公共点,求k的值;
(3)若k=﹣2m+2,直线l与抛物线的对称轴相交于点D,点P在对称轴上.当PD=PC时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某斜拉索大桥,主索塔呈抛物线,主索塔底部在水面部分的宽度AB=50米,主索塔的最高点E距水面的垂直距离为100米,桥面CD距水面的咨度为36米,则桥的宽度CD_____米.
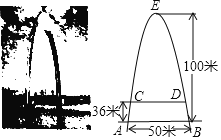
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(![]() ),B(
),B(![]() ),C(
),C(![]() )三点.
)三点.
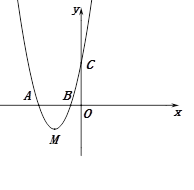
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足![]() ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com