
【题目】如图,在Rt△ABC的纸片中,∠C=90°,AC=5,AB=13.点D在边BC上,以AD为折痕将△ADB折叠得到△ADB′,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是___.
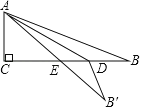
【答案】7或![]() .
.
【解析】
由勾股定理可以求出BC的长,由折叠可知对应边相等,对应角相等,当△DEB′为直角三角形时,可以分为两种情况进行考虑,分别利用勾股定理可求出BD的长.
在Rt△ABC中,![]() ,
,
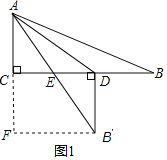
(1)当∠EDB′=90°时,如图1,
过点B′作B′F⊥AC,交AC的延长线于点F,
由折叠得:AB=AB′=13,BD=B′D=CF,
设BD=x,则B′D=CF=x,B′F=CD=12﹣x,
在Rt△AFB′中,由勾股定理得:
![]() ,
,
即:x2﹣7x=0,解得:x1=0(舍去),x2=7,
因此,BD=7.
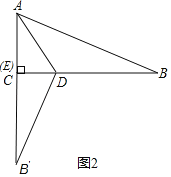
(2)当∠DEB′=90°时,如图2,此时点E与点C重合,
由折叠得:AB=AB′=13,则B′C=13﹣5=8,
设BD=x,则B′D=x,CD=12﹣x,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,解得:
,解得:![]() ,
,
因此![]() .
.
故答案为:7或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,3),点D在抛物线上且横坐标为2.
(1)求这条抛物线的表达式;
(2)将该抛物线向下平移,使得新抛物线的顶点G在x轴上.原抛物线上一点M平移后的对应点为点N,如果△AMN是以MN为底边的等腰三角形,求点N的坐标;
(3)若点P为抛物线上第一象限内的动点,过点B作BE⊥OP,垂足为E,点Q为y轴上的一个动点,连接QE、QD,试求QE+QD的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了推进教育均衡发展,在乡镇中心学校开设的体育选修课有A﹣篮球,B﹣足球,C﹣排球,D﹣羽毛球,E﹣乒乓球,学生可根据自己的爱好选修一门,学校张老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图):
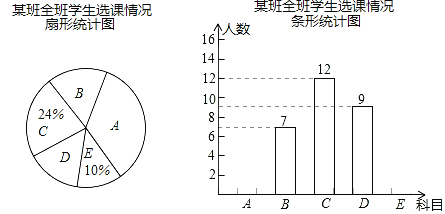
(1)求出该班的总人数,并补全条形统计图;
(2)求出“足球”在扇形统计图中的圆心角是多少度;
(3)若该班所在的年级共有1200人,请估计选篮球的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A:白开水,B:瓶装矿泉水,C:碳酸饮料,D:非碳酸饮料,根据统计结果绘制如下两个不完整的统计图,根据统计图提供的信息,解答下列问题:
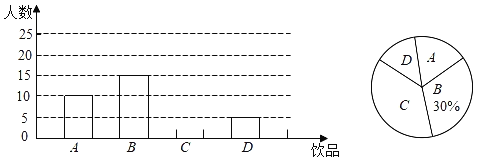
(1)这个班级有 名同学;并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如表),则该班同学每天用于饮品的人均花费是多少元?

(3)在饮用白开水的同学中有4名班委干部,为了养成良好的生活习惯,班主任决定在这4名班委干部(其中有两位班长记为A,B,其余两位记为C,D)中随机抽取2名作为良好习惯监督员,请用列表法或画树状图的方法,求出恰好抽到2名班长的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”期间,老张在某商场购物后,参加了出口处的抽奖活动.抽奖规则如下:每张发票可摸球一次,每次从装有大小形状都相同的1个白球和2个红球的盒子中,随机摸出一个球,若摸出的是白球,则获得一份奖品;若摸出的是红球,则不获奖.
(1)求每次摸球中奖的概率;
(2)老张想“我手中有两张发票,那么中奖的概率就翻了一倍.”你认为老张的想法正确吗?用列表法或画树形图分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(2)下表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
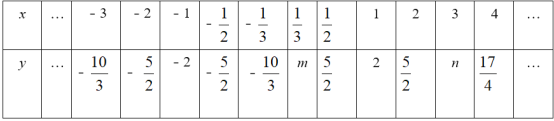
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x= .
时,x= .
②写出该函数的一条性质 .
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是 .
=t有两个不相等的实数根,则t的取值范围是 .
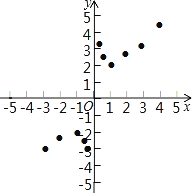
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半轻的⊙O与AC相切于点D,BD平分∠ABC,∠ABC=60°.
(1)求∠C的度数;
(2)若圆的半径OB=2,求线段CD的长度.
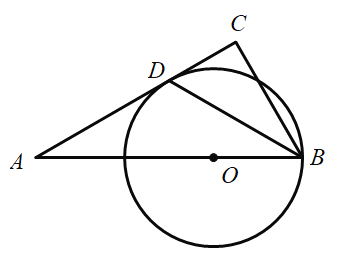
查看答案和解析>>
科目:初中数学 来源: 题型:
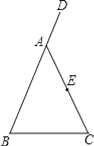
【题目】如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+(m﹣1)x+m的对称轴为x=![]() ,请你解答下列问题:
,请你解答下列问题:
(1)m= ,抛物线与x轴的交点为 .
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y<0?
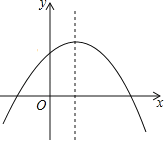
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com