
【题目】如图,已知抛物线y=﹣x2+(m﹣1)x+m的对称轴为x=![]() ,请你解答下列问题:
,请你解答下列问题:
(1)m= ,抛物线与x轴的交点为 .
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y<0?
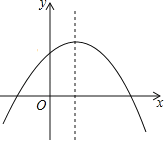
【答案】(1)2;(﹣1,0),(2,0);(2)x>![]() ;(3)x<﹣1或x>2
;(3)x<﹣1或x>2
【解析】
(1)利用抛物线的对称轴方程得到![]() =
=![]() ,解方程得到m的值,从而得到y=x2+x+2,然后解方程x2+x+2=0得抛物线与x轴的交点;(2)根据二次函数的性质求解;(3)结合函数图象,写出抛物线在x轴下方所对应的自变量的范围即可.
,解方程得到m的值,从而得到y=x2+x+2,然后解方程x2+x+2=0得抛物线与x轴的交点;(2)根据二次函数的性质求解;(3)结合函数图象,写出抛物线在x轴下方所对应的自变量的范围即可.
解:(1)抛物线的对称轴为直线x=![]() =
=![]() ,
,
∴m=2,
抛物线解析式为y=﹣x2+x+2,
当y=0时,﹣x2+x+2=0,解得x1=﹣1,x2=2,
∴抛物线与x轴的交点为(﹣1,0),(2,0);
(2)由函数图象可知,
当x>![]() 时,y的值随x的增大而减小;
时,y的值随x的增大而减小;
(3)由函数图象可知,
当x<﹣1或x>2时,y<0.


科目:初中数学 来源: 题型:
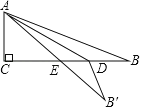
【题目】如图,在Rt△ABC的纸片中,∠C=90°,AC=5,AB=13.点D在边BC上,以AD为折痕将△ADB折叠得到△ADB′,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
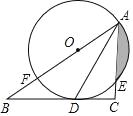
【题目】如图,在Rt△ABC中,![]() ,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
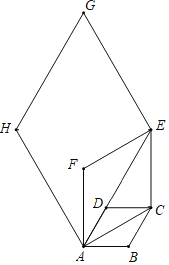
【题目】 如图,边长为1的菱形ABCD中,∠DAB=60°,连接AC,以AC为边在AC上方作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边在AE上方作第三个菱形AEGH,使∠HAE=60°.则菱形AEGH的周长为( )
A.![]() B.12C.3D.
B.12C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,正方形ABCD的边长为6,点E,点F分别在边AB,AD上,AE=DF=2,连接DE,CF交于点G.连接AC与DE交于点M,延长CB至点K,使BK=3,连接GK交AB于点N.
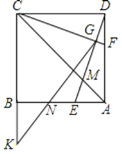
(1)求证:CF⊥DE;
(2)求△AMD的面积;
(3)请直接写出线段GN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
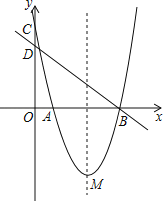
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与两坐标轴分别交于点A、B、C,直线y=﹣![]() x+4经过点B,与y轴交点为D,M(3,﹣4)是抛物线的顶点.
x+4经过点B,与y轴交点为D,M(3,﹣4)是抛物线的顶点.
(1)求抛物线的解析式.
(2)已知点N在对称轴上,且AN+DN的值最小.求点N的坐标.
(3)在(2)的条件下,若点E与点C关于对称轴对称,请你画出△EMN并求它的面积.
(4)在(2)的条件下,在坐标平面内是否存在点P,使以A、B、N、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P'是边AB上一点,四边形P'Q'M'N'是正方形,点Q',![]() 在边BC上,点N'在△ABC内.连接BN',并延长交AC于点N,NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
在边BC上,点N'在△ABC内.连接BN',并延长交AC于点N,NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
(1)求证:四边形PQMN为正方形;
(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.
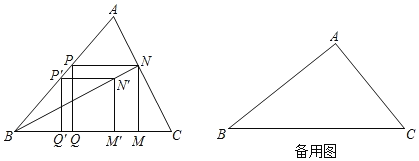
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2020年新冠肺炎疫情期间,我市某企业为支援湖北,准备将购买的70吨蔬菜运往武汉,现有甲、乙两种货车可以租用,已知2辆甲货车和3辆乙货车一次可运44吨蔬菜;3辆甲货车和1辆乙货车一次可运38吨蔬菜.
(1)求每辆甲种货车和每辆乙种货车一次分别能运多少吨蔬菜?
(2)已知甲种货车每辆租金500元,乙种货车每辆租金450元,该企业共租用甲、乙两种货车8辆,设租甲种货车a辆,求租车总费用w(元)与a之间的函数关系式,并求出自变量a的取值范围;
(3)在(2)的条件下,请你为该企业设计出费用最少的方案,并求出最少的租车费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A1的坐标为(1,0),以OA1为直角边作Rt△OA1A2,并使∠A1OA2=60°,再以OA2为直角边作Rt△OA2A3,并使∠A2OA3=60°,再以OA3为直角边作Rt△OA3A4,并使∠A3OA4=60°…按此规律进行下去,则点A2020的坐标为____.
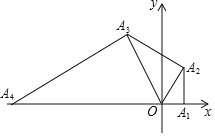
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com