
°æƒø°ø–°√˜∏˘æ›—ßœ∞∫Ø ˝µƒæ≠—È£¨∂‘∫Ø ˝y£Ωx+![]() µƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø£Æ
µƒÕºœÛ”Ζ‘÷ Ω¯––¡ÀÃΩæø£Æ
œ¬√Ê «–°√˜µƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£∫
£®1£©∫Ø ˝y£Ωx+![]() µƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß «°° °°£Æ
µƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œß «°° °°£Æ
£®2£©œ¬±Ì¡–≥ˆ¡Ày”Îxµƒº∏◊È∂‘”¶÷µ£¨«Î–¥≥ˆm£¨nµƒ÷µ£∫m£Ω°° °°£¨n£Ω°° °°£ª
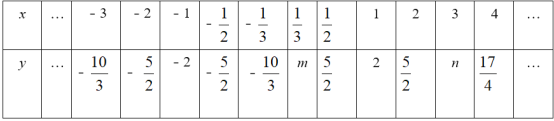
£®3£©»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨√Ë≥ˆ¡À“‘…œ±Ì÷–∏˜∂‘∂‘”¶÷µŒ™◊¯±Íµƒµ„£¨∏˘æ›√Ë≥ˆµƒµ„£¨ª≠≥ˆ∏√∫Ø ˝µƒÕºœÛ£ª
£®4£©Ω·∫œ∫Ø ˝µƒÕºœÛ£¨«ÎÕÍ≥…£∫
¢Ÿµ±y£Ω©Å![]() ±£¨x£Ω°° °°£Æ
±£¨x£Ω°° °°£Æ
¢⁄–¥≥ˆ∏√∫Ø ˝µƒ“ªÃı–‘÷ °° °°£Æ
¢€»Ù∑Ω≥Ãx+![]() £Ωt”–¡Ω∏ˆ≤ªœ‡µ»µƒ µ ˝∏˘£¨‘Útµƒ»°÷µ∑∂Œß «°° °°£Æ
£Ωt”–¡Ω∏ˆ≤ªœ‡µ»µƒ µ ˝∏˘£¨‘Útµƒ»°÷µ∑∂Œß «°° °°£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() £ª£®3£©º˚Ω‚Œˆ£ª£®4£©¢Ÿ©Å4ªÚ
£ª£®3£©º˚Ω‚Œˆ£ª£®4£©¢Ÿ©Å4ªÚ![]() £ª¢⁄ÕºœÛ‘⁄“ª£¨»˝œÛœfi£¨«“πÿ”⁄‘≠µ„∂‘≥∆£ª¢€
£ª¢⁄ÕºœÛ‘⁄“ª£¨»˝œÛœfi£¨«“πÿ”⁄‘≠µ„∂‘≥∆£ª¢€![]() ªÚ
ªÚ![]()
°æΩ‚Œˆ°ø
£®1£©”…x‘⁄∑÷ƒ∏…œ£¨ø…µ√≥ˆx°Ÿ0£ª
£®2£©∞—x£Ω![]() °¢3∑÷±¥˙»Îy£Ωx+
°¢3∑÷±¥˙»Îy£Ωx+![]() º¥ø…«Û≥ˆm°¢nµƒ÷µ£ª
º¥ø…«Û≥ˆm°¢nµƒ÷µ£ª
£®3£©¡¨µ„≥…œflº¥ø…ª≠≥ˆ∫Ø ˝ÕºœÛ£ª
£®4£©¢Ÿ∞—y£Ω©Å![]() ¥˙»Î∫Ø ˝πÿœµ Ω£¨Ω‚∑Ω≥ú¥ø…«Û≥ˆx÷µ£ª
¥˙»Î∫Ø ˝πÿœµ Ω£¨Ω‚∑Ω≥ú¥ø…«Û≥ˆx÷µ£ª
¢⁄ø…¥”∫Ø ˝ÕºœÛµƒŒª÷√∫Õ∂‘≥∆–‘µƒΩ«∂»Ω‚¥£ª
¢€ø…“‘¿˚”√∫Ø ˝ÕºœÛ£¨’“≥ˆ∫Ø ˝y£Ωx+![]() ”Îy£Ωt”–¡Ω∏ˆΩªµ„ ±tµƒ»°÷µ∑∂Œßº¥ø…£Æ
”Îy£Ωt”–¡Ω∏ˆΩªµ„ ±tµƒ»°÷µ∑∂Œßº¥ø…£Æ
Ω‚£∫£®1£©°flx‘⁄∑÷ƒ∏…œ£¨°‡x°Ÿ0£Æ
π ¥∞∏Œ™£∫x°Ÿ0£ª
£®2£©µ±x£Ω![]() ±£¨y£Ωx+
±£¨y£Ωx+![]() £Ω
£Ω![]() £ª
£ª
µ±x£Ω3 ±£¨y£Ωx+![]() £Ω
£Ω![]() £Æ
£Æ
π ¥∞∏Œ™£∫![]() £ª
£ª![]() £ª
£ª
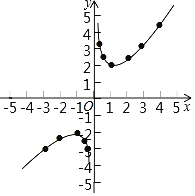
£®3£©∫Ø ˝ÕºœÛ»ÁÕºÀ˘ 棪
£®4£©¢Ÿµ±y£Ω©Å![]() ±£¨”–x+
±£¨”–x+![]() £Ω©Å
£Ω©Å![]() £¨
£¨
Ω‚µ√£∫x1£Ω©Å4£¨x2£Ω©Å![]() £Æ
£Æ
π ¥∞∏Œ™£∫©Å4ªÚ©Å![]() £ª
£ª
¢⁄π€≤Ï∫Ø ˝ÕºœÛø…÷™£∫∫Ø ˝ÕºœÛ‘⁄µ⁄“ª°¢»˝œÛœfi«“πÿ”⁄‘≠µ„∂‘≥∆£Æ
π ¥∞∏Œ™£∫∫Ø ˝ÕºœÛ‘⁄µ⁄“ª°¢»˝œÛœfi«“πÿ”⁄‘≠µ„∂‘≥∆£Æ
¢€°flx+![]() £Ωt”–¡Ω∏ˆ≤ªœ‡µ»µƒ µ ˝∏˘£¨º¥∫Ø ˝y£Ωx+
£Ωt”–¡Ω∏ˆ≤ªœ‡µ»µƒ µ ˝∏˘£¨º¥∫Ø ˝y£Ωx+![]() ”Îy£Ωt”–¡Ω∏ˆΩªµ„£¨
”Îy£Ωt”–¡Ω∏ˆΩªµ„£¨
°‡”…ÕºœÛø…µ√£∫t£º©Å2ªÚt£æ2£Æ
π ¥∞∏Œ™£∫t£º©Å2ªÚt£æ2£Æ



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄æÿ–Œ![]() ÷–£¨
÷–£¨![]() £¨µ„
£¨µ„![]() «
«![]() ±fl…œµƒ“ª∏ˆ∂ص„£¨Ω´Àƒ±fl–Œ
±fl…œµƒ“ª∏ˆ∂ص„£¨Ω´Àƒ±fl–Œ![]() —ÿ÷±œfl
—ÿ÷±œfl![]() ’€µ˛£¨µ√µΩÀƒ±fl–Œ
’€µ˛£¨µ√µΩÀƒ±fl–Œ![]() £¨µ„
£¨µ„![]() °¢
°¢![]() µƒ∂‘”¶µ„∑÷±Œ™µ„
µƒ∂‘”¶µ„∑÷±Œ™µ„![]() °¢
°¢![]() £Æ÷±œfl
£Æ÷±œfl![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £Æ
£Æ
£®1£©«Û÷§£∫![]() £ª
£ª
£®2£©¡¨Ω”![]() £¨“—÷™
£¨“—÷™![]() £Æ
£Æ
¢Ÿ»ÁÕº¢Ÿ£¨µ±![]() £¨
£¨![]() ±£¨«Û
±£¨«Û![]() µƒ≥§∂»£ª
µƒ≥§∂»£ª
¢⁄»ÁÕº¢⁄£¨µ±Àƒ±fl–Œ![]() Œ™¡‚–Œ ±£¨«Î÷±Ω”–¥≥ˆ
Œ™¡‚–Œ ±£¨«Î÷±Ω”–¥≥ˆ![]() µƒ≥§∂»£Æ
µƒ≥§∂»£Æ
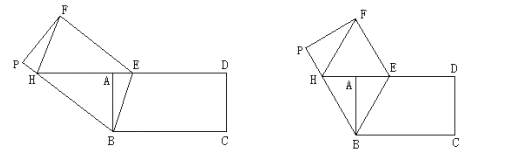
Õº¢Ÿ Õº¢⁄
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨µ„O «°œABC∫Õ°œACB¡Ω∏ˆƒ⁄Ω«∆Ω∑÷œflµƒΩªµ„£¨π˝µ„O◊˜EF°ŒBC∑÷±ΩªAB£¨AC”⁄µ„E£¨F£¨“—÷™°˜ABCµƒ÷‹≥§Œ™8£¨BC£Ωx£¨°˜AEFµƒ÷‹≥§Œ™y£¨‘Ú±Ì æy”Îxµƒ∫Ø ˝ÕºœÛ¥Û÷¬ «£®°°°°£©
A.  B.
B. 
C.  D.
D. 
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂‘”⁄“ª∏ˆ∫Ø ˝£¨◊‘±‰¡øx»°a ±£¨∫Ø ˝÷µy“≤µ»”⁄a£¨Œ“√«≥∆aŒ™’‚∏ˆ∫Ø ˝µƒ≤ª∂ص„.»Áπ˚∂˛¥Œ∫Ø ˝y£Ωx2+2x+c”–¡Ω∏ˆœ‡“ϵƒ≤ª∂ص„x1°¢x2£¨«“x1£º1£ºx2£¨‘Úcµƒ»°÷µ∑∂Œß «( )
A. c£º©Å3B. c£º©Å2C. c£º![]() D. c£º1
D. c£º1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABCµƒ÷Ω∆¨÷–£¨°œC£Ω90°„£¨AC£Ω5£¨AB£Ω13£Æµ„D‘⁄±flBC…œ£¨“‘ADŒ™’€∫€Ω´°˜ADB’€µ˛µ√µΩ°˜ADB°‰£¨AB°‰”αflBCΩª”⁄µ„E£Æ»Ù°˜DEB°‰Œ™÷±Ω«»˝Ω«–Œ£¨‘ÚBDµƒ≥§ «___£Æ
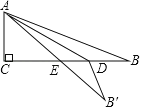
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝∑Ω–ŒABCDµƒ±fl≥§Œ™6£¨µ„E «BCµƒ÷–µ„£¨¡¨Ω”AE”Î∂‘Ω«œflBDΩª”⁄µ„G£¨¡¨Ω”CG≤¢—”≥§£¨ΩªAB”⁄µ„F£¨¡¨Ω”DEΩªCF”⁄µ„H£¨¡¨Ω”AH£Æ“‘œ¬Ω·¬€£∫¢ŸCF°ÕDE£ª¢⁄![]() £ª¢€AD£ΩAH£ª¢‹GH£Ω
£ª¢€AD£ΩAH£ª¢‹GH£Ω![]() £¨∆‰÷–’˝»∑Ω·¬€µƒ–Ú∫≈ «__________£Æ
£¨∆‰÷–’˝»∑Ω·¬€µƒ–Ú∫≈ «__________£Æ
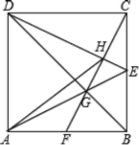
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨–°¡¡Œ™¡À≤‚¡ø–£‘∞¿ÔΩ×߬•ABµƒ∏fl∂»£¨Ω´≤‚Ω«“«CD ˙÷±∑≈÷√‘⁄”ÎΩ×߬•ÀÆ∆Ω懿Ό™18![]() mµƒµÿ√Ê…œ£¨»Ù≤‚Ω«“«µƒ∏fl∂»Œ™1.5m£¨≤‚µ√Ω×߬•µƒ∂•≤øA¥¶µƒ—ˆΩ«Œ™30°„£¨‘ÚΩ×߬•µƒ∏fl∂» «£®°°°°°°°° £©
mµƒµÿ√Ê…œ£¨»Ù≤‚Ω«“«µƒ∏fl∂»Œ™1.5m£¨≤‚µ√Ω×߬•µƒ∂•≤øA¥¶µƒ—ˆΩ«Œ™30°„£¨‘ÚΩ×߬•µƒ∏fl∂» «£®°°°°°°°° £©

A.55.5mB.54mC.19.5mD.18m
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
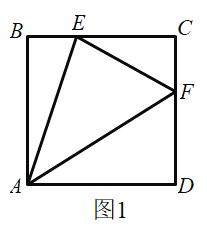
°æƒø°ø£®1£©»ÁÕº1£¨‘⁄’˝∑Ω–Œ![]() ÷–£¨µ„
÷–£¨µ„![]() °¢
°¢![]() ∑÷± «
∑÷± «![]() °¢
°¢![]() ±fl…œµƒ∂ص„£¨«“
±fl…œµƒ∂ص„£¨«“![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £Æ
£Æ
°°°°°°
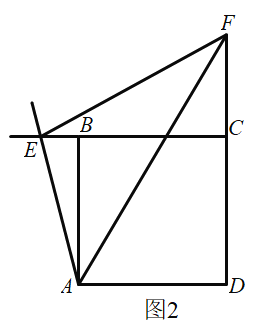
£®2£©»ÁÕº2£¨‘⁄’˝∑Ω–Œ![]() ÷–£¨»Áπ˚µ„
÷–£¨»Áπ˚µ„![]() °¢
°¢![]() ∑÷± «
∑÷± «![]() °¢
°¢![]() —”≥§œfl…œµƒ∂ص„£¨«“
—”≥§œfl…œµƒ∂ص„£¨«“![]() £¨‘Ú
£¨‘Ú![]() °¢
°¢![]() °¢
°¢![]() ÷ƺ‰ ˝¡øπÿœµ « ≤√¥£ø«Î–¥≥ˆ÷§√˜π˝≥ãÆ
÷ƺ‰ ˝¡øπÿœµ « ≤√¥£ø«Î–¥≥ˆ÷§√˜π˝≥ãÆ
£®3£©»ÁÕº1£¨»Ù’˝∑Ω–Œ![]() µƒ±fl≥§Œ™6£¨
µƒ±fl≥§Œ™6£¨![]() £¨«Û
£¨«Û![]() µƒ≥§£Æ
µƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
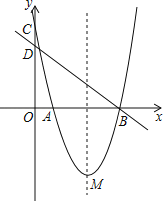
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœfly£Ωax2+bx+c”ΡΩ◊¯±Í÷·∑÷±Ωª”⁄µ„A°¢B°¢C£¨÷±œfly£Ω©Å![]() x+4æ≠π˝µ„B£¨”Îy÷·Ωªµ„Œ™D£¨M£®3£¨©Å4£© «≈◊ŒÔœflµƒ∂•µ„£Æ
x+4æ≠π˝µ„B£¨”Îy÷·Ωªµ„Œ™D£¨M£®3£¨©Å4£© «≈◊ŒÔœflµƒ∂•µ„£Æ
£®1£©«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£Æ
£®2£©“—÷™µ„N‘⁄∂‘≥∆÷·…œ£¨«“AN+DNµƒ÷µ◊Ó–°£Æ«Ûµ„Nµƒ◊¯±Í£Æ
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨»Ùµ„E”ε„Cπÿ”⁄∂‘≥∆÷·∂‘≥∆£¨«Îƒ„ª≠≥ˆ°˜EMN≤¢«ÛÀ¸µƒ√ʪ˝£Æ
£®4£©‘⁄£®2£©µƒÃıº˛œ¬£¨‘⁄◊¯±Í∆Ω√ʃ⁄ «∑ҥʑ⁄µ„P£¨ π“‘A°¢B°¢N°¢PŒ™∂•µ„µƒÀƒ±fl–Œ «∆Ω––Àƒ±fl–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Pµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com