
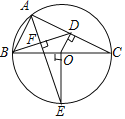
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,OD⊥AC于点D,连接BD,半径OE⊥BC,连接EA,EA⊥BD于点F.若OD=2,则BC=_____.
【答案】4![]() .
.
【解析】
根据垂径定理得到AD=DC,由等腰三角形的性质得到AB=2OD=2×2=4,得到∠BAE=∠CAE=![]() ∠BAC=
∠BAC=![]() ×90°=45°,求得∠ABD=∠ADB=45°,求得AD=AB=4,于是得到DC=AD=4,根据勾股定理即可得到结论.
×90°=45°,求得∠ABD=∠ADB=45°,求得AD=AB=4,于是得到DC=AD=4,根据勾股定理即可得到结论.
∵OD⊥AC,
∴AD=DC,
∵BO=CO,
∴AB=2OD=2×2=4,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵OE⊥BC,
∴∠BOE=∠COE=90°,
∴![]() ,
,
∴∠BAE=∠CAE=![]() ∠BAC=
∠BAC=![]() ×90°=45°,
×90°=45°,
∵EA⊥BD,
∴∠ABD=∠ADB=45°,
∴AD=AB=4,
∴DC=AD=4,
∴AC=8,
∴BC=![]() =
=![]() =4
=4![]() .
.
故答案为:4![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )

A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1、图2、图3、…图n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动.
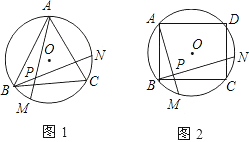
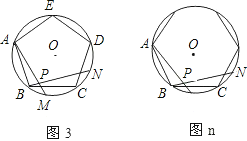
(1)求图1中∠APN的度数;
(2)求图2中,∠APN的度数,求图3中∠BPN的度数;
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点A在第四象限y1=﹣![]() 的图象上,点B在第一象限y2=
的图象上,点B在第一象限y2=![]() 的图象上,AB交x轴于点E,点C与点D在y轴上,AD=
的图象上,AB交x轴于点E,点C与点D在y轴上,AD=![]() ,S矩形OCBE=
,S矩形OCBE=![]() S矩形ODAE.
S矩形ODAE.
(1)求点B的坐标.
(2)若点P在x轴上,S△BPE=3,求直线BP的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
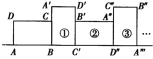
【题目】如图,在矩形ABCD中,已知AB=8,BC=6,矩形ABCD在直线上绕其右下角的顶点B向右旋转90°至矩形A′BC′D′的位置,再绕右下角的顶点C′继续向右旋转90°至矩形A′′B′C′D′′的位置,……,以此类推,这样连续旋转2 019次后,顶点A在整个旋转过程中所经过的路线之和是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增进亲子关系,丰富学生的生活,学校九年级(1)班家委会组织学生、家长一起参加户外拓展活动,所联系的旅行社收费标准如下:如果人数不超过24,人均活动费用为120元;如果人数超过24,每增加1人,人均活动费用降低2元,但人均活动费用不得低于85元,活动结束后,该班共支付该旅行社活动费用3 520元,请问该班共有多少人参加这次旅行活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民俗旅游村为接待游客住宿需要,开设了有![]() 张床位的旅馆,当每张床位每天收费
张床位的旅馆,当每张床位每天收费![]() 元时,床位可全部租出.若每张床位每天收费提高
元时,床位可全部租出.若每张床位每天收费提高![]() 元,则相应的减少了
元,则相应的减少了![]() 张床位租出.如果每张床位每天以
张床位租出.如果每张床位每天以![]() 元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 14元 B. 15元 C. 16元 D. 18元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①频率是反映事件发生的频繁程度,概率反映事件发生的可能性大小;②做n次随机试验,事件A发生m次,则事件A发生的概率一定等于![]() ;③频率是不能脱离具体的n次试验的实验值,而概率是具有确定性的不依赖于试验次数的理论值;④频率是概率的近似值,概率是频率的稳定值.其中正确的是______(填序号).
;③频率是不能脱离具体的n次试验的实验值,而概率是具有确定性的不依赖于试验次数的理论值;④频率是概率的近似值,概率是频率的稳定值.其中正确的是______(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com