
【题目】画出二次函数![]() 的图象.
的图象.
(1)利用图象求方程![]() 的近似很(结渠精确到
的近似很(结渠精确到![]() );
);
(2)设该抛物线的顶点为M,它与直线y=-3的两个交点分别为C、D,求△MCD的面积.
【答案】(1)x=1.4或3.4;(2)![]() ;
;
【解析】
(1)根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
(2)解方程x2-2x-5=-3,根据根与系数的关系得出x1+x2=2,x1x2=-2,因为抛物线与直线y=-3的两个交点C、D的横坐标就是方程的两个根,所以进而求得CD=|x1-x2|=
![]() ,然后根据三角形的面积公式求得即可.
,然后根据三角形的面积公式求得即可.
方程x22x5=0根是函数y=x22x5与x轴交点的横坐标。
作出二次函数y=x22x5的图象,如图所示,
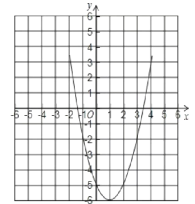
(1)由图象可知方程有两个根,一个在2和1之间,另一个在3和4之间.
先求2和1之间的根,
当x=1.4时,y=0.24;当x=1.5时,y=0.25;
因此,x=1.4是方程的一个近似根,
同理,x=3.4是方程的另一个近似根.
故一元二次方程x22x5=0的近似根为x=1.4或3.4.
(2)根据题意,得x22x5=3,
整理得x22x2=0,
∴x1+x2=2,x1x2=2,
∴CD=|x1x2|=![]()
∴在△CDM中,S△CDM=![]()
∴三角形CDM的面积是![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ACD中,CD=1,AC=3.以AD为直径作⊙O,点C恰在圆上,点B为射线CD上一点,连接BA交⊙O于点E,连接CE交AD于点G,过点A作AF∥CD交DE的延长线于点F.
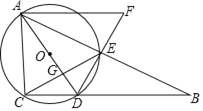
(1)若∠DAE=30°,求DE的长;
(2)求证:△AEC∽△FAD;
(3)当△GEA∽△FAD时,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1、图2、图3、…图n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动.
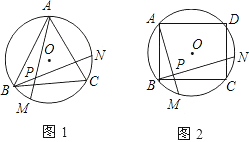
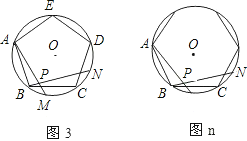
(1)求图1中∠APN的度数;
(2)求图2中,∠APN的度数,求图3中∠BPN的度数;
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
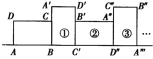
【题目】如图,在矩形ABCD中,已知AB=8,BC=6,矩形ABCD在直线上绕其右下角的顶点B向右旋转90°至矩形A′BC′D′的位置,再绕右下角的顶点C′继续向右旋转90°至矩形A′′B′C′D′′的位置,……,以此类推,这样连续旋转2 019次后,顶点A在整个旋转过程中所经过的路线之和是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增进亲子关系,丰富学生的生活,学校九年级(1)班家委会组织学生、家长一起参加户外拓展活动,所联系的旅行社收费标准如下:如果人数不超过24,人均活动费用为120元;如果人数超过24,每增加1人,人均活动费用降低2元,但人均活动费用不得低于85元,活动结束后,该班共支付该旅行社活动费用3 520元,请问该班共有多少人参加这次旅行活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
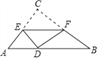
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.翻折∠C,使点C落在斜边上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若△CEF与△ABC相似,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民俗旅游村为接待游客住宿需要,开设了有![]() 张床位的旅馆,当每张床位每天收费
张床位的旅馆,当每张床位每天收费![]() 元时,床位可全部租出.若每张床位每天收费提高
元时,床位可全部租出.若每张床位每天收费提高![]() 元,则相应的减少了
元,则相应的减少了![]() 张床位租出.如果每张床位每天以
张床位租出.如果每张床位每天以![]() 元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 14元 B. 15元 C. 16元 D. 18元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
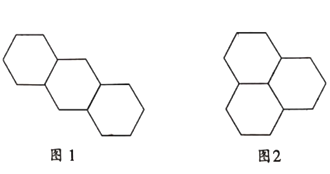
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是_______.有![]() 个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则
个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
的图象经过(1,0),(-2,3)两点,且与y轴交于点A。
(1)求直线![]() 的表达式;
的表达式;
(2)过点A做平行于x轴的直线l,l与抛物线![]() (a>0)交于B,C两点。若BC≥4,求a的取值范围;
(a>0)交于B,C两点。若BC≥4,求a的取值范围;
(3)设直线![]() 与抛物线
与抛物线![]() 交于D,E两点,当3
交于D,E两点,当3![]() ≤DE≤5
≤DE≤5![]() 时,结合函数的图象,直接写出m的取值范围是____________________。
时,结合函数的图象,直接写出m的取值范围是____________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com