
【题目】如图1,用篱笆靠墙围成矩形花围ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
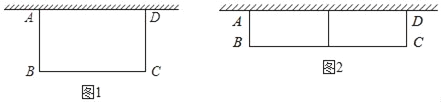
(1)若围成的花圃面积为40米2时,求BC的长;
(2)如图2若计划在花圃中间用一道隔成两个小矩形,且围成的花圃面积为50米2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由.
【答案】(1) BC的长为4米;(2) 不能围成,理由见解析.
【解析】
(1)由于篱笆总长为24m,设平行于墙的BC边长为x m,由此得到![]() ,接着根据题意列出方程
,接着根据题意列出方程![]() ,解方程即可求出BC的长;
,解方程即可求出BC的长;
(2)不能围成花圃;设BC的长为y米,则AB的长为![]() 米,
米,![]() ,此方程的判别式△=(-24)2-4×150<0,由此得到方程无实数解,所以不能围成花圃;
,此方程的判别式△=(-24)2-4×150<0,由此得到方程无实数解,所以不能围成花圃;
(1)设BC的长度为x米,则AB的长度为![]() 米,
米,
根据题意得:x![]() =40,
=40,
整理得:x2﹣24x+80=0,
解得:x1=4,x2=20.
∵20>15,
∴x2=20舍去.
答:BC的长为4米.
(2)不能围成,理由如下:
设BC的长为y米,则AB的长为![]() 米,
米,
根据题意得:y ![]() =50,
=50,
整理得:y2﹣24y+150=0.
∵△=(﹣24)2﹣4×1×150=﹣24<0,
∴该方程无实数根,
∴不能围成面积为50米2的花圃.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某超市销售樱桃,已知樱桃的进价为15元/千克,如果售价为20元/千克,那么每天可售出250千克,如果售价为25元/千克,那么每天可售出200千克,经调查发现:每天的销售量y(千克)与售价x(元/千克)之间 存在一次函数关系.
(1)求y与x之间的函数关系式;
(2)若该超市每天要获得利润810元,同时又要让消费者得到实惠,则售价x应定于多少元?
(3)若樱桃的售价不得高于28元/千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
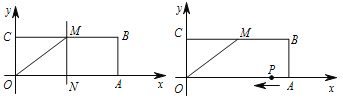
【题目】如图,矩形 ![]() 的顶点
的顶点 ![]() 、
、![]() 、
、![]() 都在坐标轴上,点
都在坐标轴上,点 ![]() 的坐标为
的坐标为 ![]() ,
,![]() 是
是 ![]() 边的中点.
边的中点.
(1)求出点 ![]() 的坐标和
的坐标和 ![]() 的周长;(直接写出结果)
的周长;(直接写出结果)
(2)若点 ![]() 是矩形
是矩形 ![]() 的对称轴
的对称轴 ![]() 上的一点,使以
上的一点,使以 ![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求出符合条件的点
为顶点的四边形是平行四边形,求出符合条件的点 ![]() 的坐标;
的坐标;
(3)若 ![]() 是
是 ![]() 边上一个动点,它以每秒
边上一个动点,它以每秒 ![]() 个单位长度的速度从
个单位长度的速度从 ![]() 点出发,沿
点出发,沿 ![]() 方向向点
方向向点 ![]() 匀速运动,设运动时间为
匀速运动,设运动时间为 ![]() 秒.是否存在某一时刻,使以
秒.是否存在某一时刻,使以 ![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似或全等? 若存在,求出此时
相似或全等? 若存在,求出此时 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点C在线段AB上,若满足AC2=BCAB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
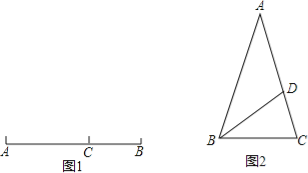
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店对文具进行组合销售,甲种组合:2支红色圆珠笔,4支黑色圆珠笔;乙种组合:3支红色圆珠笔,8支黑色圆珠笔,1个笔记本;丙种组合:2支红色圆珠笔,6支黑色圆珠笔,1个笔记本.已知红色圆珠笔每支2元,黑色圆珠笔每支1.5元,笔记本每个10元.某个周末销售这三种组合文具共485元,其中红色圆珠笔的销售额为116元,则笔记本的销售额为________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com