
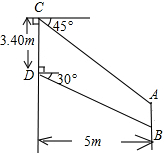
 我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414) 分析 作BF⊥CD于F,CE⊥BA于E,则CFBE是矩形,BF=CE=5,根据机翼的面积=S矩形CFBE-S△ACE-S△BDF即可计算.
解答 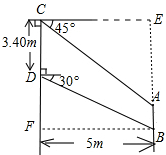 解:作BF⊥CD于F,CE⊥BA于E,则CFBE是矩形,BF=CE=5,
解:作BF⊥CD于F,CE⊥BA于E,则CFBE是矩形,BF=CE=5,
在RT△ACE中,∵∠E=90°,∠ACE=45°,
∴∠ACE=∠EAC=45°,
∴EC=EA=5,S△ACE=$\frac{25}{2}$,
在RT△BDF中,∵∠BFD=90°,∠DBF=30°,BF=5,
∴DF=BF•tan30°=$\frac{5\sqrt{3}}{3}$≈2.887,
∴S△BDF=$\frac{1}{2}$•DF•BF=7.218,
∴机翼的面积=S矩形CFBE-S△ACE-S△BDF=5(3.4+2.887)-$\frac{25}{2}$-7.218≈11.72m2.
点评 本题考查解直角三角形的应用、矩形的性质、特殊角的三角函数等知识,解题的关键是利用分割法求面积,学会转化的思想,把不规则图形的面积转化为规则图形的面积,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
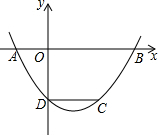 如图,抛物线y=ax2-4ax+c(a、c为常数)与x轴交于点A、B,与y轴交于点D,CD∥x轴.与抛物线交于点C,若点A的坐标为(-1,0).则线段OB与线段CD的长度的和为9.
如图,抛物线y=ax2-4ax+c(a、c为常数)与x轴交于点A、B,与y轴交于点D,CD∥x轴.与抛物线交于点C,若点A的坐标为(-1,0).则线段OB与线段CD的长度的和为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
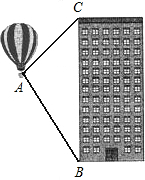 热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,这栋高楼的高是100米,A处与高楼的水平距离是50($\sqrt{3}$-1)米.
热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,这栋高楼的高是100米,A处与高楼的水平距离是50($\sqrt{3}$-1)米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com