
����Ŀ������ABC�У���ACB=90����AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E��

��1����ֱ��MN�Ƶ�C��ת��ͼ��1����λ��ʱ����Ȼ�У�DE=AD+BE����֤����
��2����ֱ��MN�Ƶ�C��ת��ͼ��2����λ��ʱ����֤��DE=AD-BE��
��3����ֱ��MN�Ƶ�C��ת��ͼ��3����λ��ʱ�����ʣ�2����DE��AD��BE�Ĺ�ϵ������������������֤�������������������־��������ĵ�����ϵ����֤����
���𰸡���1��֤������������2��֤������������3��DE=BE��AD��
��������
��1��֤����ADC�ա�CEB��Ȼ������ȫ�������ε����ʼ��ɽ�����⣻
��2��֤����ADC�ա�CEB��Ȼ������ȫ�������ε����ʼ��ɽ�����⣻
��3����ֱ��MN�Ƶ�C��ת��ͼ��3����λ��ʱ����Ȼ��ADC�ա�CEB��Ȼ������ȫ�������ε����ʿ��Եõ�DE=BE��AD��
��1���ߡ�ABC�У���ACB=90�㣬���ACD+��BCE=90�㣬
��ֱ��MN������C����AD��MN��D��BE��MN��E��
���ADC=��CEB=90�㣬���ACD+��DAC=90�㣬���BCE=��DAC��
�ڡ�ADC�͡�CEB�У�
��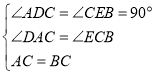 ��
��
���ADC�ա�CEB��AAS������CD=BE��AD=CE����DE=CD+CE=AD+BE��
��2���ߡ�ABC�У���ACB=90�㣬ֱ��MN������C����AD��MN��D��BE��MN��E��
���ADC=��CEB=90�㣬��ACD+��BCE=��BCE+��CBE=90�㣬
���ACD=��CBE��
��AC=BC�����ADC�ա�CEB����CD=BE��CE=AD����DE=CE��CD=AD��BE��
��3����ͼ3��
�ߡ�ABC�У���ACB=90�㣬ֱ��MN������C����AD��MN��D��BE��MN��E�����ADC=��CEB=90�㣬��ACD+��BCE=��BCE+��CBE=90�㣬���ACD=��CBE��
��AC=BC�����ADC�ա�CEB����CD=BE��CE=AD����DE=CD��CE=BE��AD��
DE��AD��BE֮��Ĺ�ϵΪDE=BE��AD��


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC�� ��M�ڡ�ABC�ڣ���P���߶�MC�ϣ���ABP��2��ACM.

(1)����PBC��10�㣬��BAC��80�������MPB��ֵ
(2)����M�ڵױ�BC�������ϣ���BP��AC����̽����A���ABP֮���������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��͵ܵ�С���ֱ�ӼҺ�ͼ���ͬʱ��������ͬһ��·������У�С�Ὺʼ�ܲ�����;��Ϊ���У�����ͼ���ǡ����30min��С�������г���300m/min���ٶ�ֱ�ӻؼң�������ҵ�·��y��m��������뿪�����ص�ʱ��x��min��֮��ĺ���������ͼ��ʾ��
��1������ͼ���֮���·��Ϊ�� ��m��С����ͼ��ݵ������õ�ʱ��Ϊ�� ����
��2����С�Ჽ��ʱy��x֮��ĺ�����ϵʽ
��3��������������ʱ�䣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
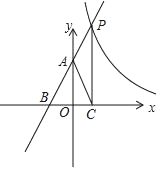
����Ŀ����֪����ͼ��ʾֱ��y=kx+2��k��0���뷴��������y=![]() ��m��0���ֱ��ڵ�P����y�ᡢx��ֱ��ڵ�A�͵�B����cos��ABO=
��m��0���ֱ��ڵ�P����y�ᡢx��ֱ��ڵ�A�͵�B����cos��ABO=![]() ����P����x��Ĵ��߽��ڵ�C������AC��
����P����x��Ĵ��߽��ڵ�C������AC��
��1����һ�κ����Ľ���ʽ��
��2����AC�ǡ�PCB�����ߣ����������Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ACB��DCE���ǵ���ֱ�������Σ���ACB=��DCE=90![]() ������AE��BD���ڵ�O. AE��DC���ڵ�M��BD��AC���ڵ�N.
������AE��BD���ڵ�O. AE��DC���ڵ�M��BD��AC���ڵ�N.
��1����ͼ�٣���֤��AE=BD��
��2����ͼ�ڣ���AC=DC���ڲ������κθ����ߵ�����£���ֱ��д��ͼ�����Ķ�ȫ�ȵ�ֱ��������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AA1��A1A2��A2A3��A3B��AB�ֱ��������Բ��ֱ������ֻС��ͬʱ����������ͬ���ٶȴӵ�A����B���׳���ADA1��A1EA2��A2FA3��A3GB·�����У��ҳ���ACB·�����У������н�����ȷ����(����)

A. ���ȵ���B B. ���ȵ���B C. �ס���ͬʱ����B D. ��ȷ��˭�ȵ���B
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����AC���ң�ֱ��EF������C��AD��EF�ڵ�D����DAC=��BAC.

��1����֤��EF����O�����ߣ�
��2����֤��AC2=AD��AB��
��3������O�İ뾶Ϊ2����ACD=300����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �İ뾶��Ϊ
�İ뾶��Ϊ![]() ��
��
![]() ����ͼ���л�����
����ͼ���л�����![]() ��
��![]() ��ʹͼ��Ϊ��Գ�ͼ�ζ��������ĶԳ�ͼ�Σ�����ͼ���л�����
��ʹͼ��Ϊ��Գ�ͼ�ζ��������ĶԳ�ͼ�Σ�����ͼ���л�����![]() ��
��![]() ��ʹͼ����Ϊ���ĶԳ�ͼ�Σ�
��ʹͼ����Ϊ���ĶԳ�ͼ�Σ�
![]() ��ͼ������
��ͼ������![]() �У�
��![]() ����
����![]() ��
��![]() ���ڵ�
���ڵ�![]() ���н�Ϊ���
���н�Ϊ���![]() �����ı���
�����ı���![]() ��������ú�
��������ú�![]() ��
��![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
![]() ���߶�
���߶�![]() ��
��![]() ��
��![]() �������ң���
�������ң���![]() ������Ϊ���Ե�
������Ϊ���Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����У��Ƿ������������ı��Σ�������ͼ��˵�����ɣ�
Ϊ������ı����У��Ƿ������������ı��Σ�������ͼ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
��1����a2b��2ab2��b3����b����a+b����a��b��������a��1��b����2��
��2���Ȼ���1+![]() ����
����![]() ���ٴө�1��0��1��2��3��ѡȡһ�����ʵ�����Ϊx��ֵ������ֵ��
���ٴө�1��0��1��2��3��ѡȡһ�����ʵ�����Ϊx��ֵ������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com