
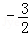 x2+
x2+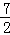 x����2����
x����2���� ��
�� ������3��
������3��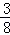
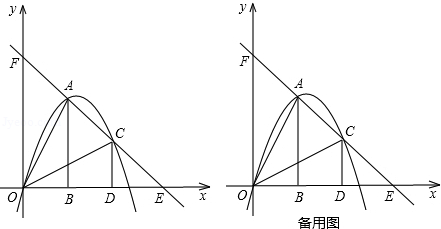
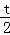 ����ɵõ�P����Ϊ��t��
����ɵõ�P����Ϊ��t��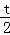 �����ɵ�M���������Ͽɵ�M��t��
�����ɵ�M���������Ͽɵ�M��t��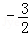 t2+
t2+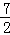 t������M����MG��AB��G����P����PH��AB��H����AG=yA��yM=2����
t������M����MG��AB��G����P����PH��AB��H����AG=yA��yM=2����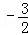 t2+
t2+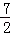 t��=
t��=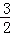 t2��
t2��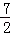 t+2��BH=PN=
t+2��BH=PN=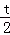 ����AG=BHʱ���ı���ABPMΪ�������Σ����ɵõ�����t�ķ��̣�������ɵõ������
����AG=BHʱ���ı���ABPMΪ�������Σ����ɵõ�����t�ķ��̣�������ɵõ������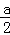 ��OH=2RH�����ɵõ���Q�����꣬�Ӷ���ʾ��A��Q�ij��������tan��O��A��B��=tan��OAB=
��OH=2RH�����ɵõ���Q�����꣬�Ӷ���ʾ��A��Q�ij��������tan��O��A��B��=tan��OAB= �����ɱ�ʾ��KT��OK������R��RH��x����H���ȱ�ʾ��S����a�ĺ�����ϵʽ���ٸ��ݶ��κ��������ʼ�����ý��.
�����ɱ�ʾ��KT��OK������R��RH��x����H���ȱ�ʾ��S����a�ĺ�����ϵʽ���ٸ��ݶ��κ��������ʼ�����ý��.
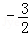 ��b=
��b=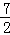 ��
��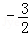 x2+
x2+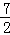 x��
x��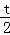
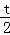 �����ߵ�M���������ϣ���M��t��
�����ߵ�M���������ϣ���M��t��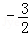 t2+
t2+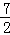 t����
t����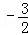 t2+
t2+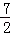 t��=
t��=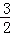 t2��
t2��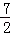 t+2��BH=PN=
t+2��BH=PN=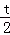 ��
��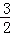 t2��
t2��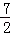 t+2=
t+2=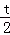 ��
�� ��
�� ��
�� ��
�� ��
�� ����ʹ���ı���ABPMΪ�������Σ�
����ʹ���ı���ABPMΪ�������Σ�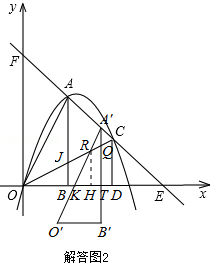
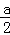 ��OH=2RH
��OH=2RH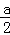 ����
����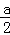 =��3��
=��3��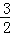 a��
a�� ��
�� =
=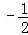 a+
a+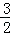 ��
��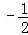 a+
a+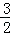 ��=
��=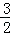 a��
a��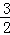 ��
��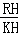 =2��
=2�� •KT•A��T��
•KT•A��T�� A��Q•HT
A��Q•HT •
•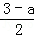 •��3��a����
•��3��a���� •��3��
•��3��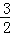 a��•����a+2��
a��•����a+2��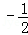 a2+
a2+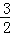 a��
a�� =
=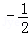 ��a��
��a��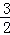 ��2+
��2+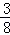
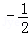 ��0��
��0��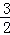 ��
��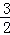 ������ʹ�ص��������Sȡ�����ֵ�����ֵΪ
������ʹ�ص��������Sȡ�����ֵ�����ֵΪ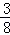 ��
��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��y=(x-2)2+3 | B��y=(x+2)2+3 | C��y=(x-2)2-3 | D��y=(x+2)2-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
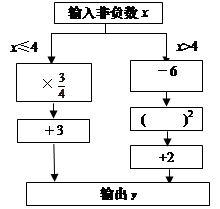
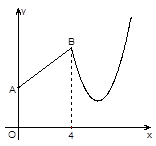
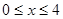 ��x��4ʱ��y��x�ĺ�����ϵʽ��
��x��4ʱ��y��x�ĺ�����ϵʽ��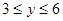 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
| ʱ��t���죩 | 1 | 3 | 6 | 10 | 36 | �� |
| ��������m������ | 94 | 90 | 84 | 76 | 24 | �� |
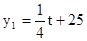 ��
�� ��tΪ����������20��ÿ��ļ۸�y2��Ԫ/������ʱ��t���죩�ĺ�����ϵʽ
��tΪ����������20��ÿ��ļ۸�y2��Ԫ/������ʱ��t���죩�ĺ�����ϵʽ 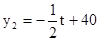 ��
�� ��tΪ������. �������Ǿ����о�����������Ʒ���й����⣺��1�������ϱ��е����ݣ�ȷ��һ��������Щ���ݵ�m��������t���죩֮��Ĺ�ϵʽ��
��tΪ������. �������Ǿ����о�����������Ʒ���й����⣺��1�������ϱ��е����ݣ�ȷ��һ��������Щ���ݵ�m��������t���죩֮��Ĺ�ϵʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
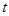 ���£�֮��Ĺ�ϵ����ǰ
���£�֮��Ĺ�ϵ����ǰ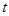 ���µ������ܺ�S��
���µ������ܺ�S��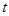 �Ĺ�ϵ��.����ͼ���ṩ����Ϣ�������������.
�Ĺ�ϵ��.����ͼ���ṩ����Ϣ�������������.
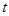 ���£�֮��ĺ�����ϵʽ��
���£�֮��ĺ�����ϵʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ����y����x�ĺ�����ͼ�����Ϊ�� ��
����y����x�ĺ�����ͼ�����Ϊ�� ��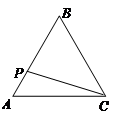
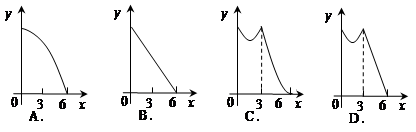
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
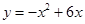 �ϣ���OA=
�ϣ���OA=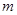 ��0��
��0��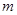 ��3��������ABCD���ܳ�Ϊ
��3��������ABCD���ܳ�Ϊ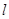 ����
����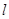 ��
�� �ĺ�������ʽΪ�� ��
�ĺ�������ʽΪ�� ��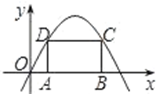
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��ͼ����
��ͼ���� ����һ�������ڣ��ͣ�֮�䣨������
����һ�������ڣ��ͣ�֮�䣨������ ��ȡֵ��Χ��( )
��ȡֵ��Χ��( )
A�� | B�� | C�� | D�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com