Question

【题目】如图，已知抛物线 的对称轴x=-1，且抛物线经过两点，与轴交于点.

⑴.若直线经过两点，求直线所在直线的解析式；

⑵.抛物线的对称轴x=-1上找一点,使点到点的距离与到点的距离之和最小，求出此点的坐标；

⑶.设点为抛物线的对称轴x=-1上的一个动点，求使△为直角三角形的点的坐标.

Answer 1

【答案】（1）y=x+3；（2）（-1，2）；（3）（-1，-2）或（-1，4）或（-1，）或（-1，）．

【解析】

试题分析：（1）先把点A，C的坐标分别代入抛物线解析式得到a和b，c的关系式，再根据抛物线的对称轴方程可得a和b的关系，再联立得到方程组，解方程组，求出a，b，c的值即可得到抛物线解析式；把B、C两点的坐标代入直线y=mx+n，解方程组求出m和n的值即可得到直线解析式；

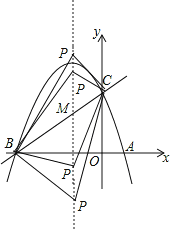
（2）设直线BC与对称轴x=-1的交点为M，则此时MA+MC的值最小．把x=-1代入直线y=x+3得y的值，即可求出点M坐标；

（3）设P（-1，t），又因为B（-3，0），C（0，3），所以可得BC2=18，PB2=（-1+3）2+t2=4+t2，PC2=（-1）2+（t-3）2=t2-6t+10，再分三种情况分别讨论求出符合题意t值即可求出点P的坐标．

试题解析：（1）依题意得：，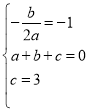

解之得：，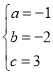

∴抛物线解析式为y=-x2-2x+3

∵对称轴为x=-1，且抛物线经过A（1，0），

∴把B（-3，0）、C（0，3）分别代入直线y=mx+n，

得，

解之得：，

∴直线y=mx+n的解析式为y=x+3；

（2）设直线BC与对称轴x=-1的交点为M，则此时MA+MC的值最小．

把x=-1代入直线y=x+3得，y=2，

∴M（-1，2），

即当点M到点A的距离与到点C的距离之和最小时M的坐标为（-1，2）；

（3）设P（-1，t），

又∵B（-3，0），C（0，3），

∴BC2=18，PB2=（-1+3）2+t2=4+t2，PC2=（-1）2+（t-3）2=t2-6t+10，

①若点B为直角顶点，则BC2+PB2=PC2即：18+4+t2=t2-6t+10解之得：t=-2；

②若点C为直角顶点，则BC2+PC2=PB2即：18+t2-6t+10=4+t2解之得：t=4，

③若点P为直角顶点，则PB2+PC2=BC2即：4+t2+t2-6t+10=18解之得：t1=，t2=；

综上所述P的坐标为（-1，-2）或（-1，4）或（-1，）或（-1，）．