
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.

求证:
(1)AD=BD;
(2)DF是⊙O的切线.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=a,点C在直线AB上,![]() .
.
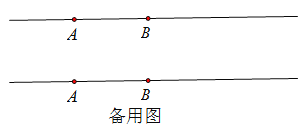
(1)用尺规作图画出点C;
(2)若点P在线段BC上,且BP:PC=2:3,D为线段PC的中点,求BD的长(用含a的代数式表示);
(3)在(2)的条件下,若AD=3cm,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在半径为R的圆形钢板上,裁去半径为r的四个小圆,当R=7.2 cm,r=1.4 cm时,剩余部分的面积是________cm2(π取3.14,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3 , 则原铁皮的边长为( )
A.10cm
B.13cm
C.14cm
D.16cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴x=-1,且抛物线经过
的对称轴x=-1,且抛物线经过![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.

⑴.若直线![]() 经过
经过![]() 两点,求直线
两点,求直线![]() 所在直线的解析式;
所在直线的解析式;
⑵.抛物线的对称轴x=-1上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出此点
的距离之和最小,求出此点![]() 的坐标;
的坐标;
⑶.设点![]() 为抛物线的对称轴x=-1上的一个动点,求使△
为抛物线的对称轴x=-1上的一个动点,求使△![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com