Question

【题目】如图，已知线段AB=a，点C在直线AB上，．

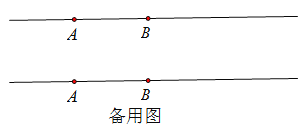
（1）用尺规作图画出点C；

（2）若点P在线段BC上，且BP：PC=2：3，D为线段PC的中点，求BD的长（用含a的代数式表示）；

（3）在（2）的条件下，若AD=3cm，求a的值．

Answer 1

【答案】（1）详见解析；（2）或；（3）或.

【解析】

试题分析：（1）分两种情况画图：点C在线段AB的延长线上或C点在线段AB的反向延长线上；

（2）对于图1，BC=2a，由BP：PC=2：3可计算出BP=BC=a，PC=BC=a，再由D为线段PC的中点得到PD=PC=a，然后利用BD=BP+PD计算得BD=a；对于图2，BC=4a，由BP：PC=2：3可计算得BP=BC=a，PC=BC=a，再由D为线段PC的中点得到PD=PC=a，然后利用BD=BP+PD计算可得BD=a；（3）对于图1，先得到CD=PD=a，再计算出AD=AC-CD=a，则a=3，然后解方程即可；对于图2，先得到CD=PD=a，利用计算出AD=BC-CD=a，则a=3，然后解方程即可．

试题解析：：解：（1）如图所示：当点C在线段AB的延长线上，如图1：

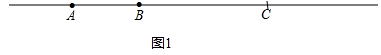
当C点在线段AB的反向延长线上时，如图2：

；

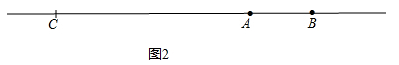（2）对于图1，

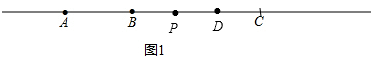
∵AB=a，∴AC=3a，∴BC=2a，

∵BP：PC=2：3，∴BP=BC=2a=a，PC=BC=a，

∵D为线段PC的中点，∴PD=PC=a，

∴BD=BP+PD=a+a=a；

对于图2，

BC=AB+AC=4a，

∵BP：PC=2：3，∴BP=BC=4a=a，PC=BC=a，

∵D为线段PC的中点，∴PD=PC=a，∴BD=BP+PD=a+a=a；

（3）对于图1，CD=PD=a，AD=AC-CD=3a-a=a=3，解得a=（cm）；

对于图2，CD=PD=a，AD=BC-CD=4a-a=a=3，解得a=（cm）．

考点:分类讨论；线段的计算；一元一次方程的应用.