
【题目】如图,∠BAC=30°,P是∠BAC平分线上一点,PM∥AC交AB于M,PD⊥AC于D,若PD=3![]() ,则AM=_______.
,则AM=_______.

【答案】![]()
【解析】
过点P作PE⊥AB于E,根据角平分线上的点到角的两边距离相等可得PD=PE,根据两直线平行,同位角相等可得∠PME=∠BAC,再根据直角三角形30°角所对的直角边等于斜边的一半可得PM=2PE,根据角平分线的定义可得∠BAP=∠CAP,根据两直线平行,内错角相等可得∠CAP=∠APM,从而得到∠BAP=∠APM,然后根据等角对等边可得AM=PM.
解:如图,过点P作PE⊥AB于E,
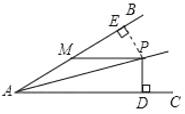
∵P是∠BAC平分线上一点,PD⊥AC,
∴PD=PE=![]() ,
,
∵PM∥AC,
∴∠PME=∠BAC=30°,
∴PM=2PE=![]() ,
,
∵P是∠BAC平分线上一点,
∴∠BAP=∠CAP,
∵PM∥AC,
∴∠CAP=∠APM,
∴∠BAP=∠APM,
∴AM=PM=![]() .
.
故答案为:![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我校一块边长为2x米的正方形空地是八年级1﹣4班的卫生区,学校把它分成大小不同的四块,采用抽签的方式安排卫生区,下图是四个班级所抽到的卫生区情况,其中1班的卫生区是一块边长为(x﹣2y)米的正方形,其中0<2y<x.

(1)分别用x、y的式子表示八年3班和八年4班的卫生区的面积;
(2)求2班的卫生区的面积比1班的卫生区的面积多多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
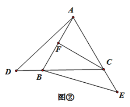
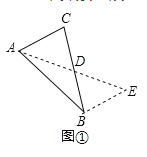
【题目】如图,△ABC是等边三角形,点D、E分别是直线BC、AC上的点,且BD=CE.
(1)如图①,当点D、E分别在线段BC、AC上时,BE与AD相交于点F.求∠AFB的度数.
(2)如图②,当点D在CB的延长线上,点E在AC的延长线上时,CF为△ABC的高线则线段CD、AF、CE、之间的数量关系是 ,并加以证明.
(3)在①的条件下,连接FC,如图③,若∠DFC=90°,AF= 3![]() ,求BF的长.
,求BF的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠C=90°,AB=5,BC=3,S、Q两点同时分别从A、C出发,点S以每秒2个单位的速度沿着AC向点C运动,点Q以每秒1个单位的速度沿着CB向点B运动.当其中一点到达终点时,另一点也随之停止运动.
(1)求经过几秒,SQ的长为2;
(2)设△SQC的面积为y,点S、Q的运动时间为x,求y与x的函数关系式,并写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com