
���� ��1����2����3�����ݷ�ĸ�����������dz˶��θ�ʽ��������ĸֻ��һ�����ԭ��ĸ���ƽ���ʽ�����˼���������ɣ�
��4���ȶ�ÿ����ʽ��ĸ��������Ȼ������Ӽ���
��� �⣺��1��$\frac{5}{\sqrt{3}}$��ĸ�������Ľ����$\frac{5\sqrt{3}}{3}$��
��2��$\frac{1}{\sqrt{6}+\sqrt{7}}$��ĸ�������Ľ����$\sqrt{7}$-$\sqrt{6}$��
��3��$\frac{1}{\sqrt{n}+\sqrt{n+1}}$��ĸ�������Ľ����$\sqrt{n+1}$-$\sqrt{n}$��
��4��$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+��+$\frac{1}{\sqrt{2015}+\sqrt{2016}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+��+$\sqrt{2016}$-$\sqrt{2015}$
=-1+12$\sqrt{14}$��
�ʴ�Ϊ��$\frac{5\sqrt{3}}{3}$��$\sqrt{7}$-$\sqrt{6}$��$\sqrt{n+1}$-$\sqrt{n}$��
���� ���⿼���˷�ĸ�����������������θ�ʽ�Ĵ���ʽ���ʱ�����ǵĻ��������θ�ʽ����������������ʽ�ɻ�Ϊ��������ʽ��һ�����θ�ʽ����������ʽ��ֹһ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
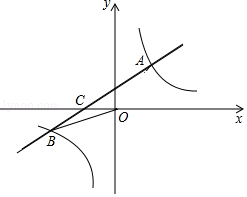 ��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=ax+b��a��b�dz�������a��0����ͼ���뷴��������$y=\frac{k}{x}$��k�dz�������k��0����ͼ����һ���������ڵ�A��B���㣬��x�ύ�ڵ�C����A������Ϊ��2��m������B������Ϊ��n��-2����tan��BOC=$\frac{2}{5}$��
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=ax+b��a��b�dz�������a��0����ͼ���뷴��������$y=\frac{k}{x}$��k�dz�������k��0����ͼ����һ���������ڵ�A��B���㣬��x�ύ�ڵ�C����A������Ϊ��2��m������B������Ϊ��n��-2����tan��BOC=$\frac{2}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 610 | B�� | 616 | C�� | 648 | D�� | 680 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ƽ������� | B�� | ���ഹֱ����� | ||
| C�� | ����ƽ�У�����ͬһ��ֱ���ϣ������ | D�� | ����ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
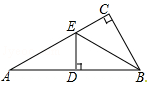 ��ͼ���ڡ�ABC�У���ACB=90�㣬BEƽ�֡�ABC��DE��AB�ڵ�D�����AC=3cm����ôAE+DE���ڣ�������
��ͼ���ڡ�ABC�У���ACB=90�㣬BEƽ�֡�ABC��DE��AB�ڵ�D�����AC=3cm����ôAE+DE���ڣ�������| A�� | 2cm | B�� | 3cm | C�� | 4cm | D�� | 5cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{CD}{AB}$ | B�� | $\frac{AC}{BC}$ | C�� | $\frac{BC}{AB}$ | D�� | $\frac{AC}{AB}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com