
分析 作BH⊥x轴于H,如图,根据等边三角形的性质得OH=AH=$\frac{1}{2}$OA=2,∠BOH=60°,利用含30度的直角三角形三边的关系得到BH=$\sqrt{3}$OH=2$\sqrt{3}$,则B(2,2$\sqrt{3}$),然后利用待定系数法求反比例函数解析式.
解答 解:作BH⊥x轴于H,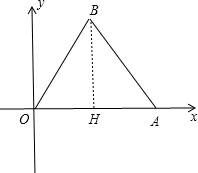 如图,
如图,
∵△OAB为等边三角形,
∴OH=AH=$\frac{1}{2}$OA=2,∠BOH=60°,
∴BH=$\sqrt{3}$OH=2$\sqrt{3}$,
∴B(2,2$\sqrt{3}$),
设反比例函数解析式为y=$\frac{k}{x}$,
把B(2,2$\sqrt{3}$)代入得k=2×2$\sqrt{3}$=4$\sqrt{3}$,
所以反比例函数解析式为y=$\frac{4\sqrt{3}}{x}$.
故答案为y=$\frac{4\sqrt{3}}{x}$.
点评 本题考查了待定系数法求反比例函数的解析式:设出含有待定系数的反比例函数解析式y=$\frac{k}{x}$(k为常数,k≠0);把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;解方程,求出待定系数;写出解析式.也考查了等边三角形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | ①③④ | B. | ①④⑤ | C. | ①②⑤ | D. | ②④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形顶角的平分线是它的对称轴 | |
| B. | 有一个内角60°的三角形是轴对称图形 | |
| C. | 等腰直角三角形是轴对称图形,它的对称轴是斜边上的中线所在的直线 | |
| D. | 等腰三角形的角平分线、中线和高重合 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间x(天) | 1≤x<45 | 45≤x≤80 |
| 售价(元/件) | x+40 | 80 |
| 每天销量(件) | 200-2x | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com