
| A. | ①③④ | B. | ①④⑤ | C. | ①②⑤ | D. | ②④⑤ |
分析 根据题意画出图形,再根据在△ABC中,已知AB=AC,∠A=36°求出∠C的度数;由线段垂直平分线的性质求出∠ABD的度数,故可得出∠DBC的度数,进而得出BD是∠ABC的平分线;由三角形内角和定理可求出∠BDC的度数;由线段垂直平分线的性质,易证得△ABD是等腰三角形.
解答 解:∵△ABC中,∠A=36°,AB=AC,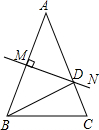
∴∠ABC=∠C=$\frac{180°-∠A}{2}$=72°,
故①正确;
∵DM是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠DBC=∠ABC-∠DBC=72°-36°=36°,
∴BD是∠ABC的平分线,
故②错误;
∵在△BCD中,∠DBC=36°,∠C=72°,
∴∠BDC=180°-(∠DBC+∠C)=180°-(36°+72°)=72°.
故③错误;
∵DM是AB的垂直平分线,
∴AD=BD
∴△ABD是等腰三角形;
故④正确;
∵MN是线段AB的垂直平分线,
∴AD=BD,
∵∠A=∠ABD=36°,
∴∠CBD=36°,
∴BD=BC,
∴AD=BD=BC,故⑤正确.
故选B.
点评 本题考查的是线段垂直平分线的性质及等腰三角形的判定与性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:选择题
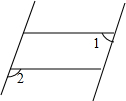 一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=70°,则∠2的大小是( )
一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=70°,则∠2的大小是( )| A. | 70° | B. | 110° | C. | 60° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
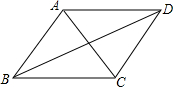 如图,下列条件之一能使平行四边形ABCD是菱形的为( )
如图,下列条件之一能使平行四边形ABCD是菱形的为( )| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com