
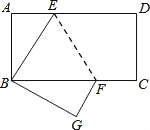
【题目】如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
【答案】(1)△BEF是等腰三角形,理由见解析;(2)10.
【解析】
(1)根据翻折不变性和平行线的性质得到两个相等的角,根据等角对等边即可判断△BEF是等腰三角形;
(2)根据翻折的性质可得BE=DE,BG=CD,∠EBG=∠ADC=90°,设BE=DE=x,表示出AE=8x,然后在Rt△ABE中,利用勾股定理列出方程求出x的值,即为BE的值,再根据同角的余角相等求出∠ABE=∠GBF,然后利用“角边角”证明△ABE和△GBF全等,根据全等三角形对应边相等可得BF=BE,再根据三角形的面积公式列式计算即可得解.
(1)△BEF是等腰三角形.
∵ED∥FC,
∴∠DEF=∠BFE,
根据翻折不变性得到∠DEF=∠BEF,
故∠BEF=∠BFE.
∴BE=BF.
△BEF是等腰三角形;
(2)∵矩形ABCD沿EF折叠点B与点D重合,
∴BE=DE,BG=CD,∠EBG=∠ADC=90°,∠G=∠C=90°,
∵AB=CD,
∴AB=BG,
设BE=DE=x,则AE=AB﹣DE=8﹣x,
在Rt△ABE中,AB2+AE2=BE2,
即42+(8﹣x)2=x2,
解得x=5,
∴BE=5,
∵∠ABE+∠EBF=∠ABC=90°,
∠GBF+∠EBF=∠EBG=90°,
∴∠ABE=∠GBF,
在△ABE和△MBF中,
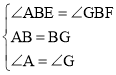 ,
,
∴△ABE≌△GBF(ASA),
∴BF=BE=5,
∴△EBF的面积=![]() ×5×4=10.
×5×4=10.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
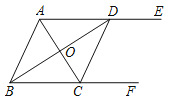
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
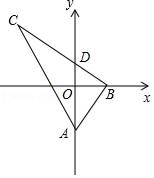
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=![]() x2﹣x+
x2﹣x+![]() 与x轴分别交于A、B两点(A点在B点的左侧),交y轴于点F.
与x轴分别交于A、B两点(A点在B点的左侧),交y轴于点F.
(1)A点坐标为 ;B点坐标为 ;F点坐标为 ;
(2)如图1,C为第一象限抛物线上一点,连接AC,BF交于点M,若BM=FM,在直线AC下方的抛物线上是否存在点P,使S△ACP=4,若存在,请求出点P的坐标,若不存在,请说明理由;
(3)如图2,D、E是对称轴右侧第一象限抛物线上的两点,直线AD、AE分别交y轴于M、N两点,若OMON=![]() ,求证:直线DE必经过一定点.
,求证:直线DE必经过一定点.
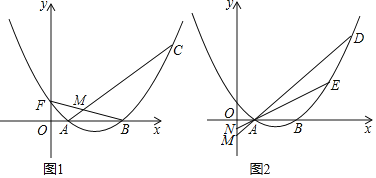
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是 ;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且![]() 时,直接写出线段CE的长.
时,直接写出线段CE的长.
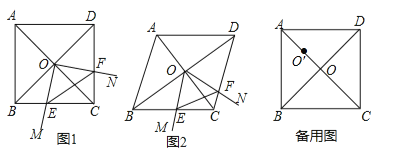
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 是
是![]() 的平均数,即
的平均数,即![]() ,则方差
,则方差![]() ,它反映了这组数的波动性,
,它反映了这组数的波动性,
(1)证明:对任意实数a,x1a,x2a,…,xna,与x1,x2,…,xn 方差相同;
(2)证明![]() ;
;
(3)以下是我校初三(1)班 10 位同学的身高(单位:厘米):
169,172,163,173,175,168,170,167,170,171,计算这组数的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 经过直线
经过直线![]() 与坐标轴的两个交点
与坐标轴的两个交点![]() .此抛物线与
.此抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() .抛物线的顶点为
.抛物线的顶点为![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 若点
若点![]() 为抛物线上一动点,是否存在点
为抛物线上一动点,是否存在点![]() .使
.使![]() 与
与![]() 的面积相等?若存在,求点
的面积相等?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我国建立了比较完善的经济困难学生资助体系.某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元,设每半年发放的资助金额的平均增长率为![]() ,则下面列出的方程中正确的是( )
,则下面列出的方程中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com