
【题目】如图,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是_____.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.
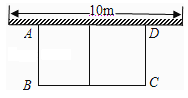
(1)求y与x的函数关系式;
(2)如果要围成面积为63m2的花圃,AB的长是多少?
(3)能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
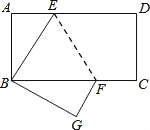
【题目】如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
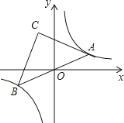
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
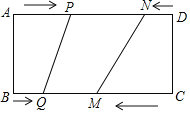
【题目】如图,在矩形ABCD中,BC=20cm,P、Q、M、N分别从A、B、C、D出发沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.
(Ⅰ)当x为何值时,AP、ND长度相等?
(Ⅱ)当x为何值时,以PQ、MN为两边,以矩形的边(AD或BC)的一部分为第三边能构成一个三角形?
(Ⅲ)当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
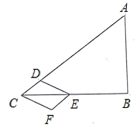
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 以
以![]() /
/![]() 的速度运动,同时动点
的速度运动,同时动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以
以![]() /
/![]() 的速度向终点
的速度向终点![]() 运动,当有一点到达终点时,另一点也停止运动,以
运动,当有一点到达终点时,另一点也停止运动,以![]() 、
、![]() 为邻边作设
为邻边作设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]()
![]() 点
点![]() 运动的时间为
运动的时间为![]() .
.
(1)当点![]() 在
在![]() 边上时,求
边上时,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在线段
落在线段![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式
之间的函数关系式![]() ,并写出自变量
,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
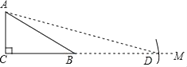
【题目】如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com