
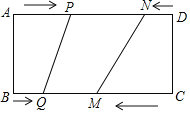
����Ŀ����ͼ���ھ���ABCD�У�BC��20cm��P��Q��M��N�ֱ��A��B��C��D������AD��BC��CB��DA�����ھ��εı���ͬʱ�˶�������һ�����ȵ��������˶��ߵ���һ���˵�ʱ��ֹͣ����֪����ͬʱ���ڣ���BQ��xcm��x��0������AP��2xcm��CM��3xcm��DN��x2cm��
����xΪ��ֵʱ��AP��ND������ȣ�
����xΪ��ֵʱ����PQ��MNΪ���ߣ��Ծ��εıߣ�AD��BC����һ����Ϊ�������ܹ���һ�������Σ�
����xΪ��ֵʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
���𰸡�����xΪ2ʱ��AP��ND������ȣ�����xΪ![]() ʱ����PQ��MNΪ���ߣ��Ծ��εıߣ�AD��BC����һ����Ϊ�������ܹ���һ�������Σ�����x��2��x��4ʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
ʱ����PQ��MNΪ���ߣ��Ծ��εıߣ�AD��BC����һ����Ϊ�������ܹ���һ�������Σ�����x��2��x��4ʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
��������
(��)������ó����̣��ⷽ�̼��ɣ�
(��)����P���N�غϻ��Q���M�غ����������������ó����̣��ⷽ�̼��ɣ�
(��) ��P��N���������������ۣ���P�ڵ�N�������P�ڵ�N���Ҳ࣬��һ������ƽ���ı��ε������������̽�ɣ�
(��)��![]() ��
��
��AP=NDʱ����![]() ��
��
��ã�![]() ��
��![]() (��ȥ)��
(��ȥ)��
�൱![]() Ϊ2ʱ��AP��ND������ȣ�
Ϊ2ʱ��AP��ND������ȣ�
(��)����P���N�غϻ��Q���M�غ�ʱ����PQ��MNΪ���ߣ��Ծ��εı�(AD��BC)��һ����Ϊ�����߿��ܹ���һ�������Σ�
������P���N�غ�ʱ��
������ã�![]() ��
��
��ã�![]() (��ȥ)��
(��ȥ)��
��![]() ����ʱ��Q���M���غϣ�
����ʱ��Q���M���غϣ�
��![]() �������⣻
�������⣻
������Q���M�غ�ʱ��
������ã�![]() ��
��
��ã�![]() ��
��
��ʱ![]() �����������⣬
�����������⣬
���Q���M�����غϣ�
��������������![]() ��ֵΪ��
��ֵΪ��![]() ��
��
(��)�ߵ�N�㵽��A��ʱ��![]() ����ʱM���Q�㻹δ������
����ʱM���Q�㻹δ������
���Qֻ���ڵ�M����࣬
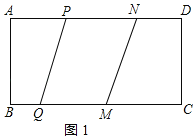
������P�ڵ�N�����ʱ����ͼ1��ʾ��
������ã�![]() ��
��
��ã�![]() (��ȥ)��
(��ȥ)��![]() ��
��
��![]() ʱ�ı���PQMN��ƽ���ı��Σ�
ʱ�ı���PQMN��ƽ���ı��Σ�
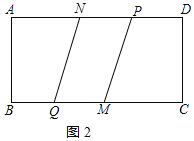
������P�ڵ�N���Ҳ�ʱ����ͼ2��ʾ��
������ã�![]() ��
��
��ã�![]() (��ȥ)��
(��ȥ)��![]() ��
��
��![]() ʱ���ı���NQMP��ƽ���ı��Σ�
ʱ���ı���NQMP��ƽ���ı��Σ�
������������![]() ��
��![]() ʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�
ʱ����P��Q��M��NΪ������ı�����ƽ���ı��Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
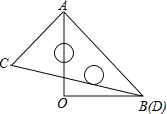
����Ŀ��һ�����ǰ尴��ͼ��ʾ������һ�����̶���AOB������ACD���Ź�������A����˳ʱ�뷽����ת���ȣ�0��������180����������ACD��һ������AOB��ijһ��ƽ��ʱ����Ӧ����ת������ֵ��___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() ��ƽ��������
��ƽ��������![]() ����
����![]() ������ӳ���������IJ����ԣ�
������ӳ���������IJ����ԣ�
��1��֤����������ʵ��a��x1a��x2a������xna����x1��x2������xn ������ͬ��
��2��֤��![]() ��
��
��3����������У������1���� 10 λͬѧ�����ߣ���λ�����ף���
169��172��163��173��175��168��170��167��170��171�������������ķ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C��
��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C��
(1)��������ߵĽ���ʽ��
(2)��ͼ�٣�����D����������һ���㣬���D�ĺ�����Ϊm��0��m��3��������CD��BD��BC��AC������BCD��������ڡ�AOC�����2��ʱ����m��ֵ��
(3)����NΪ�����߶Գ�����һ�㣬����ͼ����̽�����������Ƿ���ڵ�M��ʹ����B��C��M��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д���������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ��߶�AC�Ƶ�A��ʱ����ת�õ��߶�AF��CF��BA���ӳ��߽��ڵ�E������E����FAE����ACB��21�������ECD�Ķ�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BEƽ����ABC��AC�ڵ�E������E��ED��BC��AB�ڵ�D��
��1����֤��AEBC=BDAC��
��2�����![]() =3��
=3��![]() =2��DE=6����BC�ij���
=2��DE=6����BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�У�ÿ���������б߳�Ϊ1 ��С��������ɣ�
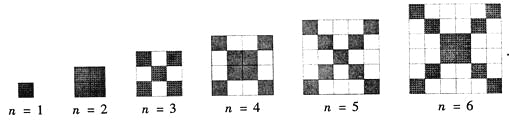
��1�� �۲�ͼ�Σ�����д���б���
�����α߳� | 1 | 3 | 5 | 7 | �� | n(����) |
��ɫС�����θ��� | �� | |||||
�����α߳� | 2 | 4 | 6 | 8 | �� | n(ż��) |
��ɫС�����θ��� | �� |
��2���ڱ߳�Ϊn��n��1�����������У����ɫС�����εĸ���ΪP1����ɫС�����εĸ���ΪP2�����Ƿ����ż��n��ʹP2��5P1�������ڣ���д��n��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
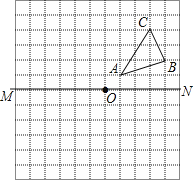
����Ŀ����ͼ����֪����ABC�������������У�
��1���뻭����ABC����O��ʱ����ת90���õ��ġ�A1B1C1��
��2���뻭����ABC���ڵ�O�ԳƵġ�A2B2C2��
��3����ֱ��MN������һ��P��ʹ��PAB���ܳ���С���뻭����PAB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y1=��x+4��y2=![]() x+b����˫����y=
x+b����˫����y=![]() ���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
��1����y��x֮��ĺ�����ϵʽ��
��2��ֱ��д����x��0ʱ������ʽ![]() x+b��
x+b��![]() �Ľ⼯��
�Ľ⼯��
��3������P��x���ϣ�����AP����ABC������ֳ�1��3�����֣����ʱ��P�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com