
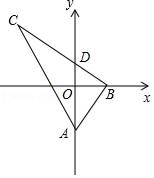
【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
【答案】C
【解析】
作CH⊥x轴于H,AC交OH于F.由△CBH∽△BAO,推出![]() ,推出BH=﹣2a,CH=2b,推出C(b+2a,2b),由题意可证△CHF∽△BOD,可得
,推出BH=﹣2a,CH=2b,推出C(b+2a,2b),由题意可证△CHF∽△BOD,可得![]() ,推出
,推出![]() ,推出FH=2c,可得C(﹣b﹣2c,2b),因为2c+2b=﹣2a,推出2b=﹣2a﹣2c,b=﹣a﹣c,可得C(a﹣c,﹣2a﹣2c),由此即可判断;
,推出FH=2c,可得C(﹣b﹣2c,2b),因为2c+2b=﹣2a,推出2b=﹣2a﹣2c,b=﹣a﹣c,可得C(a﹣c,﹣2a﹣2c),由此即可判断;
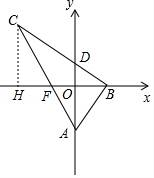
解:作CH⊥x轴于H,AC交OH于F.
∵tan∠BAC=![]() =2,
=2,
∵∠CBH+∠ABH=90°,∠ABH+∠OAB=90°,
∴∠CBH=∠BAO,∵∠CHB=∠AOB=90°,
∴△CBH∽△BAO,
∴![]() ,
,
∴BH=﹣2a,CH=2b,
∴C(b+2a,2b),
由题意可证△CHF∽△BOD,
∴![]() ,
,
∴![]() ,
,
∴FH=2c,
∴C(﹣b﹣2c,2b),
∵2c+2b=﹣2a,
∴2b=﹣2a﹣2c,b=﹣a﹣c,
∴C(a﹣c,﹣2a﹣2c),
故选:C.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】某市民广场有一个直径16米的圆形喷水池,喷水池的周边有一圈喷水头(喷水头高度忽略不计),各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合,水柱离中心3米处达最高5米,如图所示建立直角坐标系.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时必须在离水池中心O________米以内.

查看答案和解析>>
科目:初中数学 来源: 题型:
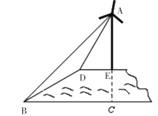
【题目】随着传统的石油、煤等自然资源逐渐消耗殆尽,风力、核能、水电等一批新能源被广泛使用.现在山顶的一块平地![]() 上建有一座风车
上建有一座风车![]() ,山的斜坡
,山的斜坡![]() 的坡度
的坡度![]() ,长是100米,在山坡的坡底
,长是100米,在山坡的坡底![]() 处测得风车顶端
处测得风车顶端![]() 的仰角为
的仰角为![]() ,在山坡的坡顶
,在山坡的坡顶![]() 处测得风车顶端
处测得风车顶端![]() 的仰角为
的仰角为![]() ,请你计算风车的高度.(结果保留根号)
,请你计算风车的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.
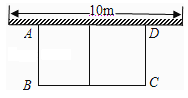
(1)求y与x的函数关系式;
(2)如果要围成面积为63m2的花圃,AB的长是多少?
(3)能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示支付方式有:![]() 微信、
微信、![]() 支付宝、
支付宝、![]() 现金、
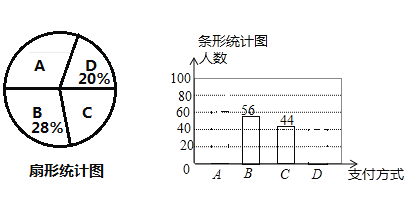
现金、![]() 其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了 名购买者?
(2)请补全条形统计图;在扇形统计图中,![]() 种支付方式所对应的圆心角为 度;
种支付方式所对应的圆心角为 度;
(3)若该超市这一周内有2000名购买者,请你估计使用![]() 和
和![]() 两种支付方式的购买者共有多少名?
两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七、八年级各有10名同学参加市级数学竞赛,各参赛选手的成绩如下(单位:分):
七年级:89,92,92,92,93,95,95,96,98,98
八年级:88,93,93,93,94,94,95,95,97,98
整理得到如下统计表
年级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
七年级 | 98 | 94 | a | m | 7.6 |
八年级 | 98 | n | 94 | 93 | 6.6 |
根据以上信息,完成下列问题
(1)填空:a= ;m= ;n= ;
(2)两个年级中, 年级成绩更稳定;
(3)七年级两名最高分选手分别记为:A1,A2,八年级第一、第二名选手分别记为B1,B2,现从这四人中,任意选取两人参加市级经验交流,请用树状图法或列表法求出这两人分别来自不同年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校检测学生跳绳水平,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图

(1)D组的人数是 人,补全频数分布直方图,扇形图中m= ;
(2)本次调查数据中的中位数落在 组;
(3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
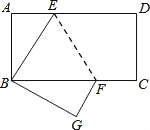
【题目】如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
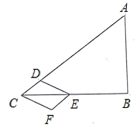
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 以
以![]() /
/![]() 的速度运动,同时动点
的速度运动,同时动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以
以![]() /
/![]() 的速度向终点
的速度向终点![]() 运动,当有一点到达终点时,另一点也停止运动,以
运动,当有一点到达终点时,另一点也停止运动,以![]() 、
、![]() 为邻边作设
为邻边作设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]()
![]() 点
点![]() 运动的时间为
运动的时间为![]() .
.
(1)当点![]() 在
在![]() 边上时,求
边上时,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在线段
落在线段![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式
之间的函数关系式![]() ,并写出自变量
,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com