
【题目】某校七、八年级各有10名同学参加市级数学竞赛,各参赛选手的成绩如下(单位:分):
七年级:89,92,92,92,93,95,95,96,98,98
八年级:88,93,93,93,94,94,95,95,97,98
整理得到如下统计表
年级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
七年级 | 98 | 94 | a | m | 7.6 |
八年级 | 98 | n | 94 | 93 | 6.6 |
根据以上信息,完成下列问题
(1)填空:a= ;m= ;n= ;
(2)两个年级中, 年级成绩更稳定;
(3)七年级两名最高分选手分别记为:A1,A2,八年级第一、第二名选手分别记为B1,B2,现从这四人中,任意选取两人参加市级经验交流,请用树状图法或列表法求出这两人分别来自不同年级的概率.
【答案】(1)94;(2)94,92,94;八;(3)![]()
【解析】
(1)根据中位数、众数和平均数的定义求解;
(2)根据方差的意义进行判断;
(3)画树状图展示所有12等可能的结果数,再找出这两人分别来自不同年级的结果数,然后利用概率公式求解.
(1)n=![]() (88+93+93+93+94+94+95+95+97+98)=94(分);
(88+93+93+93+94+94+95+95+97+98)=94(分);
把七年级的10名学生的成绩从小到大排列,最中间的两个数的平均数是:![]() =94(分),
=94(分),
则中位数a=94;
七年级的10名学生的成绩中92分出现次数最多,故众数为92分;
(2)七年级和八年级的平均数相同,但八年级的方差较小,
所以八年级的成绩稳定;
(3)列表得:
乙 甲 | A1 | A2 | B1 | B2 |
A1 | (A1,A2) | (A1,B1) | (A1,B2) | |
A2 | (A2,A1) | (A2,B1) | (A2,B2) | |
B1 | (B1,A1) | (B1,A2) | (B1,B2) | |
B2 | (B2,A1) | (B2,A2) | (B2,B1) |
共有12种等可能的结果,这两人分别来自不同年级的有8种情况,
∴P(这两人分别来自不同年级的概率)=![]() .
.


科目:初中数学 来源: 题型:
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,……,如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰5”中C的位置是有理数___,﹣2019应排在A、B、C、D、E中的___位置.其中两个填空依次为( )
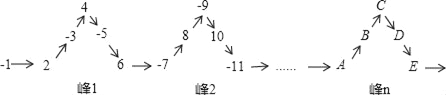
A. 24,C B. 24.A C. 25,B D. ﹣25,E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点
轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ,
,![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() .则点
.则点![]() 的坐标为( )
的坐标为( )
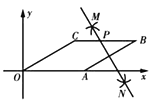
A.![]() B.
B.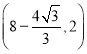 C.
C.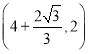 D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
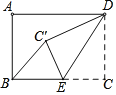
【题目】矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.
(1)求抛物线的函数表达式;
(2)如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;
(3)如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图象是函数性质的直观载体,通过图象我们容易把握函数的整体性质.下面我们就一类特殊的函数展开探究.经历分析解析式、列表、描点、连线过程得到函数![]() 、
、![]() 、
、![]() 的图象如下图所示.
的图象如下图所示.
(1)观察发现:三个函数的图象都是双曲线,且分别关于直线![]() 、
、![]() 、
、![]() 对称:三个函数解析式中分式部分完全相同,则图象的大小和形状完全相同,只有位置和对称轴发生了变化.因此,我们可以通过描点或平移的方法画函数图象.平移函数
对称:三个函数解析式中分式部分完全相同,则图象的大小和形状完全相同,只有位置和对称轴发生了变化.因此,我们可以通过描点或平移的方法画函数图象.平移函数![]() 的图象可以得到函数
的图象可以得到函数![]() 、
、![]() 的图象,分别写出平移的方向和距离.
的图象,分别写出平移的方向和距离.
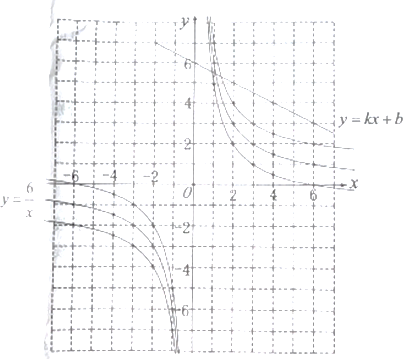
(2)探索思考:在所给的平面直角坐标系中,请用你喜欢的方法画出函数![]() 图象,并写出这个函数的一条性质.
图象,并写出这个函数的一条性质.
(3)拓展应用:若直线![]() 过点
过点![]() 、
、![]() ,结合你所画的函数图象,直接写出不等式
,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com