
【题目】已知,抛物线y=![]() x2﹣x+
x2﹣x+![]() 与x轴分别交于A、B两点(A点在B点的左侧),交y轴于点F.
与x轴分别交于A、B两点(A点在B点的左侧),交y轴于点F.
(1)A点坐标为 ;B点坐标为 ;F点坐标为 ;
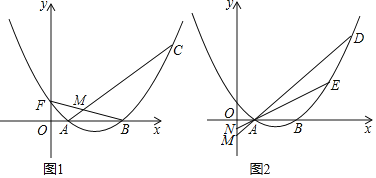
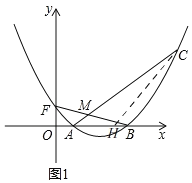
(2)如图1,C为第一象限抛物线上一点,连接AC,BF交于点M,若BM=FM,在直线AC下方的抛物线上是否存在点P,使S△ACP=4,若存在,请求出点P的坐标,若不存在,请说明理由;
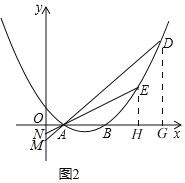
(3)如图2,D、E是对称轴右侧第一象限抛物线上的两点,直线AD、AE分别交y轴于M、N两点,若OMON=![]() ,求证:直线DE必经过一定点.
,求证:直线DE必经过一定点.
【答案】(1)(1,0),(3,0),(0,![]() );(2)在直线AC下方的抛物线上不存在点P,使S△ACP=4,见解析;(3)见解析
);(2)在直线AC下方的抛物线上不存在点P,使S△ACP=4,见解析;(3)见解析
【解析】
(1)根据坐标轴上点的特点建立方程求解,即可得出结论;
(2)在直线AC下方轴x上一点,使S△ACH=4,求出点H坐标,再求出直线AC的解析式,进而得出点H坐标,最后用过点H平行于直线AC的直线与抛物线解析式联立求解,即可得出结论;
(3)联立直线DE的解析式与抛物线解析式联立,得出![]() ,进而得出
,进而得出![]() ,
,![]() ,再由
,再由![]() 得出
得出![]() ,进而求出
,进而求出![]() ,同理可得
,同理可得![]() ,再根据
,再根据![]() ,即可得出结论.
,即可得出结论.
(1)针对于抛物线![]() ,
,
令x=0,则![]() ,
,
∴![]() ,
,
令y=0,则![]() ,
,
解得,x=1或x=3,
∴![]() ,
,
综上所述:![]() ,
,![]() ,
,![]() ;
;
(2)由(1)知,![]() ,
,![]() ,
,
∵BM=FM,
∴![]() ,
,
∵![]() ,
,
∴直线AC的解析式为:![]() ,
,
联立抛物线解析式得: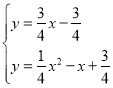 ,
,
解得: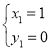 或
或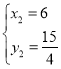 ,
,
∴![]() ,
,
如图1,设H是直线AC下方轴x上一点,AH=a且S△ACH=4,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
过H作l∥AC,
∴直线l的解析式为![]() ,
,
联立抛物线解析式,解得![]() ,
,
∴![]() ,
,
即:在直线AC下方的抛物线上不存在点P,使![]() ;
;
(3)如图2,过D,E分别作x轴的垂线,垂足分别为G,H,
设![]() ,
,![]() ,直线DE的解析式为
,直线DE的解析式为![]() ,
,
联立直线DE的解析式与抛物线解析式联立,得![]() ,
,
∴![]() ,
,![]() ,
,
∵DG⊥x轴,
∴DG∥OM,
∴![]() ,
,
∴![]() ,
,
即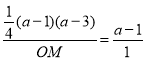 ,
,
∴![]() ,同理可得
,同理可得![]()
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴直线DE的解析式为![]() ,
,
∴直线DE必经过一定点![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:
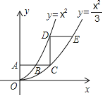
【题目】如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=![]() (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.
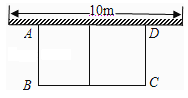
(1)求y与x的函数关系式;
(2)如果要围成面积为63m2的花圃,AB的长是多少?
(3)能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七、八年级各有10名同学参加市级数学竞赛,各参赛选手的成绩如下(单位:分):
七年级:89,92,92,92,93,95,95,96,98,98
八年级:88,93,93,93,94,94,95,95,97,98
整理得到如下统计表
年级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
七年级 | 98 | 94 | a | m | 7.6 |
八年级 | 98 | n | 94 | 93 | 6.6 |
根据以上信息,完成下列问题
(1)填空:a= ;m= ;n= ;
(2)两个年级中, 年级成绩更稳定;
(3)七年级两名最高分选手分别记为:A1,A2,八年级第一、第二名选手分别记为B1,B2,现从这四人中,任意选取两人参加市级经验交流,请用树状图法或列表法求出这两人分别来自不同年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校检测学生跳绳水平,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图

(1)D组的人数是 人,补全频数分布直方图,扇形图中m= ;
(2)本次调查数据中的中位数落在 组;
(3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.
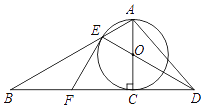
(1)求证:PE是⊙O的切线;
(2)若⊙O的半径为3,∠B=30°,求P点到直线AD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
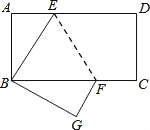
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
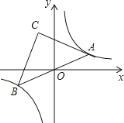
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com