
【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.
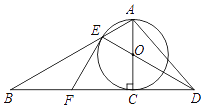
(1)求证:PE是⊙O的切线;
(2)若⊙O的半径为3,∠B=30°,求P点到直线AD的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接FO,由P为BC的中点,AO=CO,得到OP∥AB,由于AC是⊙O的直径,得出CE⊥AE,根据OP∥AB,得出OP⊥CE,于是得到OP所在直线垂直平分CE,推出PC=PE,OE=OC,再由∠ACB=90°,即可得到结论.
(2)设P点到直线AD的距离为d,记△PAD的面积S△PAD,根据三角形的面积得到d=![]() ①由勾股定理得BC=6
①由勾股定理得BC=6![]() ,根据平行线的性质得到∠OPC=∠B=30°,推出△OEA为等边三角形,得到∠EOA=60°,在Rt△ACD中,由勾股定理得:AD=
,根据平行线的性质得到∠OPC=∠B=30°,推出△OEA为等边三角形,得到∠EOA=60°,在Rt△ACD中,由勾股定理得:AD=![]() =3
=3 ![]() ,将以上数据代入①得即可得到结论.
,将以上数据代入①得即可得到结论.
(1)证明:连接CE,如图所示:
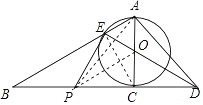
∵AC为⊙O的直径,
∴∠AEC=90°.
∴∠BEC=90°.
∵点F为BC的中点,
∴EF=BF=CF.
∴∠FEC=∠FCE.
∵OE=OC,
∴∠OEC=∠OCE.
∵∠FCE+∠OCE=∠ACB=90°,
∴∠FEC+∠OEC=∠OEF=90°.
∴EF是⊙O的切线;
(2)解:设P点到直线AD的距离为d,记△PAD的面积S△PAD,
则有:S△PAD=![]() ADd=
ADd=![]() PDAC,
PDAC,
∴d=![]() ①
①
∵⊙O的半径为3,∠B=30°,
∴∠BAC=60°,AC=6,AB=12,
由勾股定理得BC=6![]() ,
,
∴PC=3![]()
∵O,P分别是AC,BC的中点,
∴OP∥AB,
∴∠OPC=∠B=30°,
∵OE=OA,∠OAE=60°,
∴△OEA为等边三角形,
∴∠EOA=60°,
∴∠ODC=90°﹣∠COD=90°﹣∠EOA=30°,
∴∠ODC=∠OPC=30°,
∴OP=OD,
∵OC⊥PD,
∴CD=PC=3![]() ,
,
在Rt△ACD中,由勾股定理得:AD=![]() =3
=3![]() ,
,
将以上数据代入①得:d=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
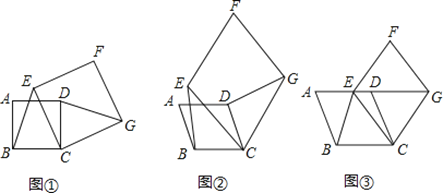
【题目】感知:如图①,四边形ABCD、CEFG均为正方形.易知BE=DG.
探究:如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
应用:如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD的延长线上.若AE=3ED, ∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
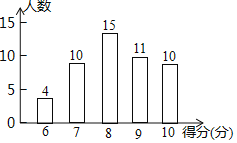
【题目】为了了解居民的环保意识,社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动,并用得到的数据绘制了如图条形统计图(得分为整数,满分为10分,最低分为6分)
请根据图中信息,解答下列问题:
(1)本次调查一共抽取了 名居民;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)社区决定对该小区500名居民开展这项有奖问答活动,得10分者设为“一等奖”,请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0(A2+B2≠0)的距离公式为:d=![]() ,
,
例如,求点P(1,3)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知:A=4,B=3,C=﹣3
所以P(1,3)到直线4x+3y﹣3=0的距离为:d=![]() =2
=2
根据以上材料,解决下列问题:
(1)求点P1(1,-1)到直线3x﹣4y﹣5=0的距离.
(2)已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣![]() x+b相切,求实数b的值;
x+b相切,求实数b的值;
(3)如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出△ABP面积的最大值和最小值.
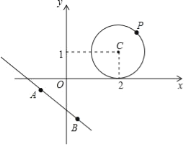
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
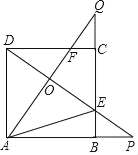
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的港珠澳大桥是目前桥梁设计中广泛采用的斜拉桥,它用粗大的钢索将桥面拉住,为检测钢索的抗拉强度,桥梁建设方从甲、乙两家生产钢索的厂方各随机选取5根钢索进行抗拉强度的检测,数据统计如下(单位:百吨)

甲、乙两厂钢索抗拉强度检测统计表
钢索 | 1 | 2 | 3 | 4 | 5 | 平均数 | 中位数 | 方差 |
甲厂 | 10 | 11 | 9 | 10 | 12 | 10.4 | 10 | 1.04 |
乙厂 | 10 | 8 | 12 | 7 | 13 | a | b | c |
(1)求乙厂5根钢索抗拉强度的平均数a(百吨)、中位数b(百吨)和方差c(平方百吨).
(2)桥梁建设方决定从抗拉强度的总体水平和稳定性来决定钢索的质量,问哪一家的钢索质量更优?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 30 | … |
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com