
【题目】某校为了解学生每周参加家务劳动的情况,随机调查了该校部分学生每周参加家务劳动的时间.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
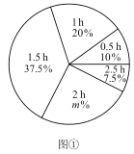

(1)本次接受调查的学生人数为___________,,图①中m的值为_________;
(2)求统计的这组每周参加家务劳动时间数据的众数、中位数和平均数;
(3)根据统计的这组每周参加家务劳动时间的样本数据,若该校共有800名学生,估计该校每周参加家务劳动的时间大于![]() 的学生人数.
的学生人数.
【答案】(1)40,25;(2)1.5,1.5,1.5;(3)560人
【解析】
(1)根据统计图中的数据求得调查的总人数,进而求得m值;
(2)根据统计图中的数据,结合平均数、众数和中位数的定义分别进行求解即可;
(3)用总人数乘以大于1h的学生人数所占的比例即可得出答案.
(1)8÷20%=40(人),10÷40=25%,
故答案为:40,25;
(2)∵在这组样本数据中,1.5出现了15次,出现的次数最多,
∴这组样本数据的众数为1.5.
∵将这组样本数据按从小到大的顺序排列,处于中间的两个数都是1.5,有![]() ,
,
∴这组样本数据的中位数为1.5.
观察条形统计图,![]() ,
,
∴这组数据的平均数是1.5;
(3)∵在统计的这组样本数据中,每周参加家务劳动时间大于![]() 的学生人数占70%,
的学生人数占70%,
∴估计该校800名初中学生中,每周参加家务劳动时间大于![]() 的人数约占70%.
的人数约占70%.
有![]() (人).
(人).
∴该校800名初中学生中,每周参加家务劳动时间大于![]() 的学生人数约为560.
的学生人数约为560.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断,其中不正确的是( )
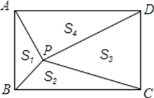
A.PA+PB+PC+PD的最小值为10
B.若△PAB≌△PCD,则△PAD≌△PBC
C.若△PAB△PDA,则PA=2
D.若S1=S2,则S3=S4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
①BF为∠ABE的角平分线;
②DF=2BF;
③2AB2=DFDB;
④sin∠BAE=![]() .其中正确的为( )
.其中正确的为( )
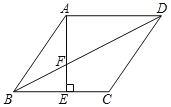
A.①③B.①②④C.①④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax.
(1)二次函数图象的对称轴是直线x= ;
(2)当0≤x≤3时,y的最大值与最小值的差为4,求该二次函数的表达式;
(3)若a<0,对于二次函数图象上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥3时,均满足y1≥y2,请结合函数图象,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() ABC中,∠ACB=45°, D为AC上一点,
ABC中,∠ACB=45°, D为AC上一点,![]() ,连接BD,将
,连接BD,将![]() ABD沿BD翻折至
ABD沿BD翻折至![]() EBD,点A的对应点E点恰好落在边BC上,延长BC至点F,连接DF,若CF=2,
EBD,点A的对应点E点恰好落在边BC上,延长BC至点F,连接DF,若CF=2,![]() ,则DF长为( )
,则DF长为( )
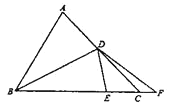
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
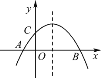
【题目】如图,已知抛物线![]() (m>0)与x轴相交于点A,B,与y轴相交于点C,且点A在点B的左侧.
(m>0)与x轴相交于点A,B,与y轴相交于点C,且点A在点B的左侧.
(1)若抛物线过点(2,2),求抛物线的解析式;
(2)在(1)的条件下,抛物线的对称轴上是否存在一点H,使AH+CH的值最小,若存在,求出点H的坐标;若不存在,请说明理由;
(3)在第四象限内,抛物线上是否存在点M,使得以点A,B,M为顶点的三角形与△ACB相似?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
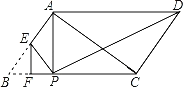
【题目】如图,AC是ABCD的对角线,∠BAC=90°,![]() ABC的边AB,AC,BC的长是三个连续偶数,E,F分别是边AB,BC上的动点,且EF⊥BC,将
ABC的边AB,AC,BC的长是三个连续偶数,E,F分别是边AB,BC上的动点,且EF⊥BC,将![]() BEF沿着EF折叠得到
BEF沿着EF折叠得到![]() PEF,连接AP,DP.若
PEF,连接AP,DP.若![]() APD为直角三角形时,BF的长为_____.
APD为直角三角形时,BF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
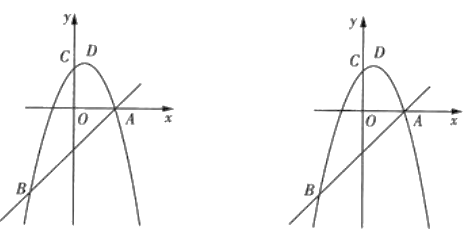
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)若向下平移抛物线,使顶点![]() 落在
落在![]() 轴上,原来的抛物线上的点
轴上,原来的抛物线上的点![]() 平移后的对应点为
平移后的对应点为![]() .若
.若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上是否存在点![]() 使
使![]() 的面积是
的面积是![]() 面积的一半?若存在,直接写出点
面积的一半?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com