
【题目】如图1,在平面直角坐标系中Rt△AOB≌Rt△DCA,其中B(0,4),C(2,0).连接BD.

(1)求直线BD的解析式;
(2)点E是直线AD上一点,连接BE,以BE,ED为一组邻边作BEDF,当BEDF的面积为3时,求点E的坐标;
(3)如图2,将△DAC沿x轴向左平移,平移距离大于0,记平移后的△DAC为△D′A′C′,连接D′A,D′B,当△D′AB为等腰三角形时,直接写出点D′的坐标.
【答案】(1)直线BD的表达式为:y=﹣x+4;(2)点E的坐标为(1,![]() )或(3,
)或(3,![]() );(3)点D′的坐标为(﹣6,2)或(﹣4,2).
);(3)点D′的坐标为(﹣6,2)或(﹣4,2).
【解析】
(1)![]() ,则AO=CD,OB=AC=4,
,则AO=CD,OB=AC=4,![]() ,则点
,则点![]() ,即可求解;
,即可求解;
(2)设直线![]() 交
交![]() 轴于点
轴于点![]() ,则点
,则点![]() ,利用
,利用![]() ,即可求解;
,即可求解;
(3)分![]() 、
、![]() 、
、![]() ,求解即可.
,求解即可.
解:(1)![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() ,
,
将![]() 、
、![]() 坐标代入一次函数:
坐标代入一次函数:![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
故直线![]() 的表达式为:
的表达式为:![]() ,
,
同理直线![]() 的表达式为:
的表达式为:![]() ;
;
(2)①当点![]() 在线段
在线段![]() 上时,
上时,
设直线![]() 交
交![]() 轴于点
轴于点![]() ,则点
,则点![]() ,
,

![]() ,
,
即:![]() ,
,
解得:![]() ,即点
,即点![]() ,
,
②当点![]() 在线段
在线段![]() 外时,
外时,
同理可得:点![]() ,
,
故点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
(3)设图象向左平移![]() 个单位,则点
个单位,则点![]() ,
,
则:![]() ,
,![]() ,
,![]() ,
,
当![]() 时,即:
时,即:![]() ,
,
解得:![]() ,
,![]() 刚好是在线段
刚好是在线段![]() 上,所以形成不了三角形,故舍去;
上,所以形成不了三角形,故舍去;
当![]() 时,同理可得:
时,同理可得:![]() ,
,
当![]() 时,同理可得:
时,同理可得:![]() ,
,
故:点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF、DE、EF与AC交于点O,DE与交于点G,连接OG,若![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③EF⊥AC;④
;③EF⊥AC;④![]() .其中正确的结论的序号是___________.
.其中正确的结论的序号是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
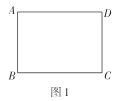
综合与实践课上,老师让同学们以“折纸”为主题开展数学活动.如图1,有一张长为4,宽为3的矩形纸片![]() (
(![]() ).
).
操作发现
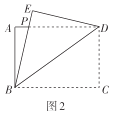
(1)快乐小组先将图1中的矩形纸片![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在点
落在点![]() 处,得到图2,他们发现
处,得到图2,他们发现![]() ,请你证明这个结论;
,请你证明这个结论;
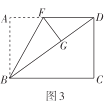
(2)创新小组将图2中的矩形纸片展开后继续折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,得到图3,则折痕
,得到图3,则折痕![]() __________;
__________;
实践探究
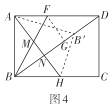
(3)前进小组在创新小组的操作基础上,将图3中的纸片展开,再将矩形纸片![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,然后将纸片展平.如图4所示,折痕
处,然后将纸片展平.如图4所示,折痕![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,试判断
,试判断![]() 的形状并证明你的结论.
的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐角△ABC 中,BC=6,BC 边上的高 AD=4,两动点 M,N 分别在边 AB,AC 上滑动(M 不与 A、B 重合),且 MN∥BC,以 MN 为边向下作正方形 MPQN,设其边长为 x,正方形 MPQN 与△ABC 公共部分的面积为 y(y>0).
(1)MN,BC具备什么条件,△AMN∽△ABC;
(2)当 x为何值时,PQ 恰好落在边 BC 上(如图 1);
(3)当 PQ 在△ABC 外部时(如图 2),求 y 关于 x 的函数关系式(注明 x 的取值范围)并求出 x 为何值时 y 最大,最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:
(1)求直线AC的解析式;
(2)求△OAC的面积;
(3)是否存在点M、使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标;若不存在,请说明理由?
?若存在,求出此时点M的坐标;若不存在,请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com